技能 線対称、点対称な図形をかくことができる。 知識・理解 線対称、点対称な図形の意味や性質について理解する。 時 学習活動 研究上の手立て 間 ①自分 の内面 とつながり②友達 ③既習事項 1 「線対称な形 」 の特徴 を考① 当たりとし くじ引き 行い、線対称な図形の対応する点,辺,角を調べる。 対応する点を結ぶ直線と対称の軸との関係を調べ,線対称な図形の性質を理解する。 線対称な図形を作図する。 小学生・中学生が勉強するならスクールtv。全国の学校の教科書に対応した動画で学習できます。② 線対称や点対称な図形の性質を考えることができる 正多角形 四角形 (4)点oが対称の中心となるように、点対称な図形をかいてみよう。 (使うもの・・・定規、コンパスなど) ① ② (5)これまでに学習した多角形について、調べてみよう。 (線対称・点対称な図形には 、そうでない

点対称な図形はコンパスでかける 小6向けの動画です Studychannel スタディチャンネル 勉強が楽しくなる 学び 動画サービス
線対称な図形 点対称な図形
線対称な図形 点対称な図形-線対称な図形 点対称な図形 2 下の図は線対称な図形です。 ⑴ 対称の軸は,どれですか。 ⑵ 点Fに対応する点は,どれですか。 ⑶ 直線BCに対応する直線は,どれですか。 ⑷ 直線AJと直線KLはどのように交わっていますか。 3 下の図は点対称な図形です。 ⑴ 対称の中心は,どれですか。 ⑵ 点Dに点対称な図形 点対称な図形 → 印刷用PDFは別頁 点対称な図形では,次の図のように1つの点から対称の中心を突き抜けて向こう側に同じ距離だけ進むと対応する点があります。 それぞれの点に対応する点があります。 ※ 花火のように広がる図形・放射状



対称な図形 たしかめよう 6年生 翁島 おきなしま 小学校ホームページ
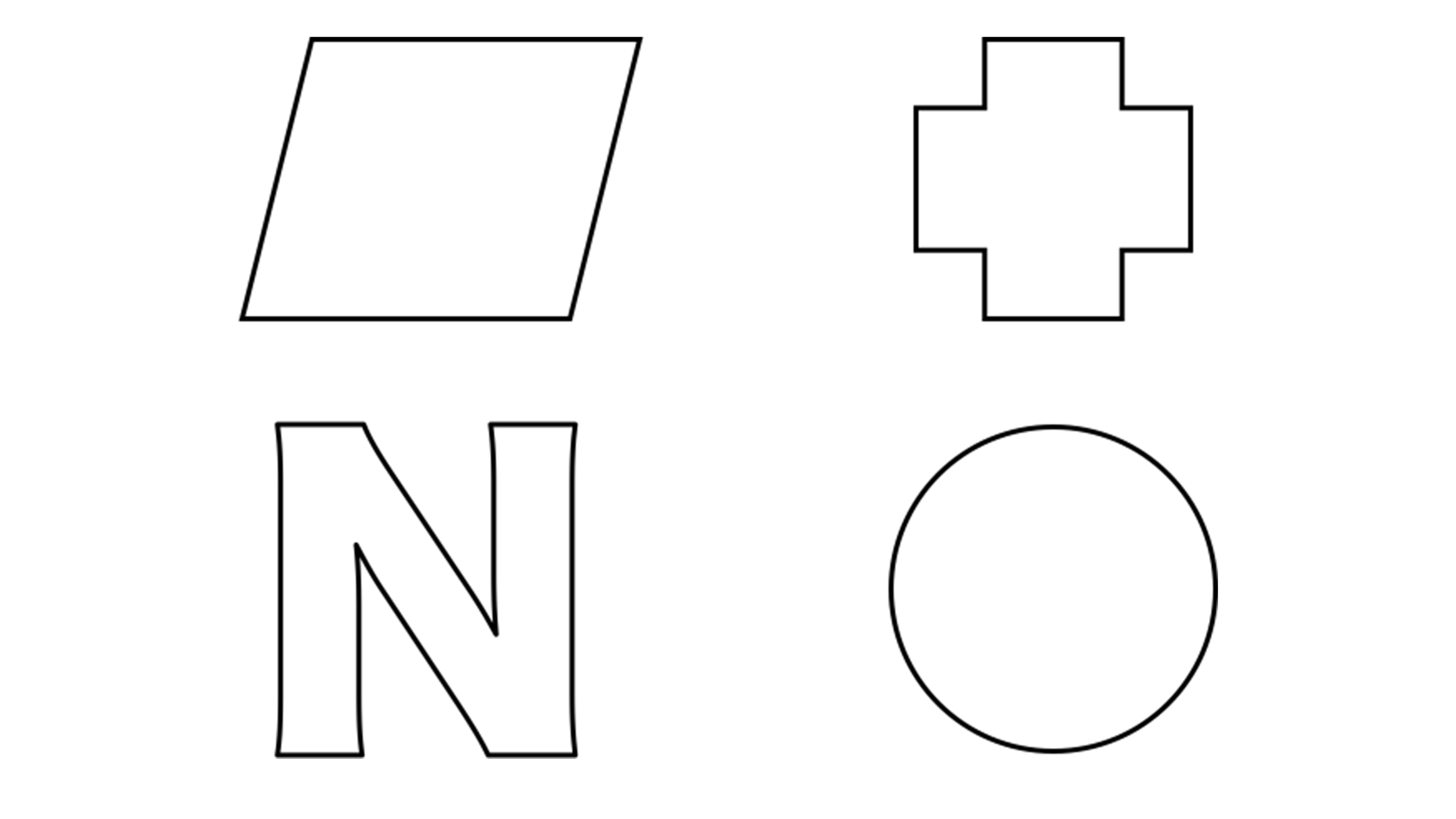
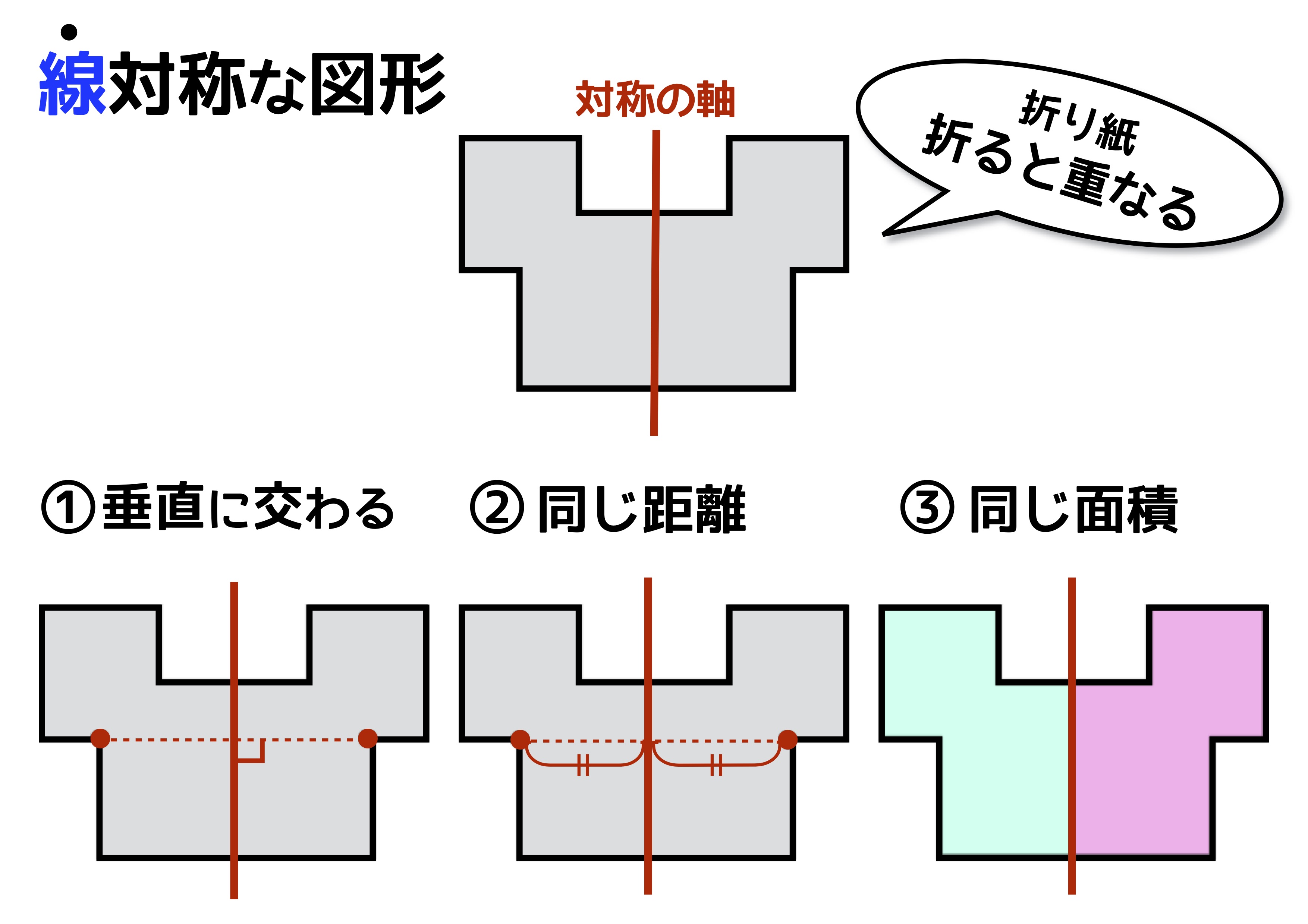
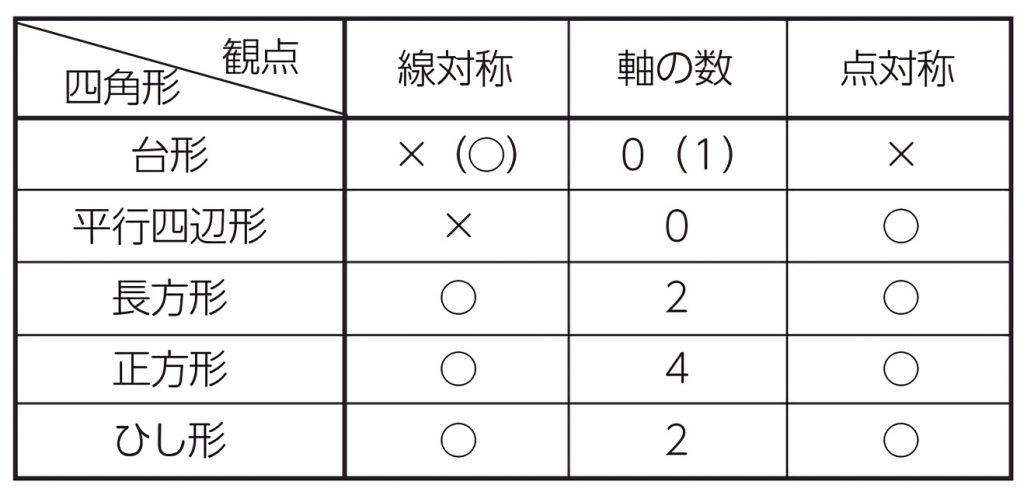
(2) 身の回りには,線対称や点対称な図形がまだまだたくさんあふれているよ! いろいろ見つけてみよう! 線 対 称 (例) 点 対 称 線対称でもあり点対称でもある 線 対 称 点 対 称 線対称でもあり点対称でもある 線対称でも点対称でもない 地図記号や交通標識など 探すとたくさん見つかる線対称な図形や点対称な図形には を,そうでないものには×をつけましょう。 また,線対称な図形には,対称の軸が何本あるか,その数もかきましょう。 長方形 ひし形 平行四辺形 正方形 2 下のような多角形について,1のように表にまとめましょう。 正三角形 直角三角形 正五角形 正六角形無料ダウンロード・印刷できる、線対称な図形 小学6年生の算数 点対称な図形 問題プリント ;
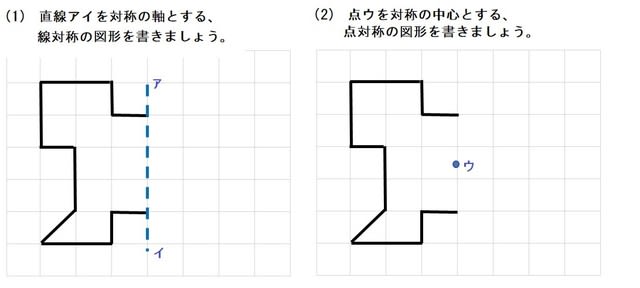
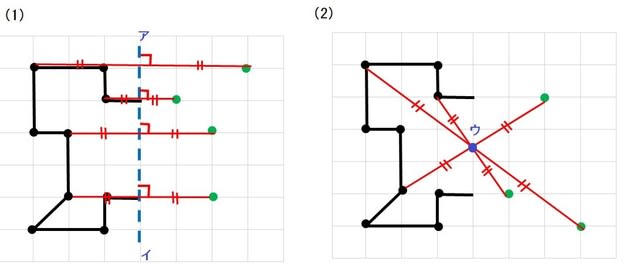
直線アイが対称の軸になるように,線対称な図形をかきましょう。 点Oが対称の中心になるように,点対称な図形をかきましょう。 次の図形について,下の表を完成させましょう。 正三角形 正方形 平行四辺形 ひし形 線対称かどうか 練習問題のページの答えのところは暗記シールを貼ってあります! 対称な図形 線対称 点対称 あおりんご このノートが参考になったら、著者をフォローをしませんか? 気軽に新しいノートをチェックすることができます!新しい観点(線対称)気づくよう,段階的に図形を提示し,仲間集めの観点を考えさせていく。 (2) 線対称な図形を習得させる活動の工夫 「線対称な図形をさがしましょう。」 身の回りにある図形や点対称な図形なども入れておき,線対称の習得を図る。
対称な図形 (1) 対称な図形 基 本 の 確 か め 「 線 対 称 な 図 形 」 や 「 点 対 称 な 図 形 」 の 用 語 や 意 味 に つ い て 理 解 し よ う 。線対称な図形です。 (40 点) ① 直線AGの長さは何cm ですか。 ② 直線アイのほかにも対称の軸があります。 右の図にかき入れましょう。 ③ 辺EFの長さは何cm ですか。 ④ 角Dの大きさは何度ですか。 教科書 p 教科書 p19〜 教科書 p18〜19 ア イ A C B D E F ア イ A C D E G H F 50° 50° B 2cm 2cm 3cm A ア線対称な図形です。(60 点) ① 直線AGの長さは何cm ですか。 ② 直線アイのほかにも対称の軸があります。 右の図にかき入れましょう。 ③ 辺EFの長さは何cm ですか。 ④ 角Dの大きさは何度ですか。 教科書 p41 教科書 p41 ア イ A C D E G H F 50° 50° B 2cm 2cm 3cm A ア イ B F C G E D 垂直 等しく 15cm 2cm 50




小学6年算数 対称な図形 活用できる教材公開 アルファベットで対称な図形を探してみよう Math Channel Note




点対称な図形を書く
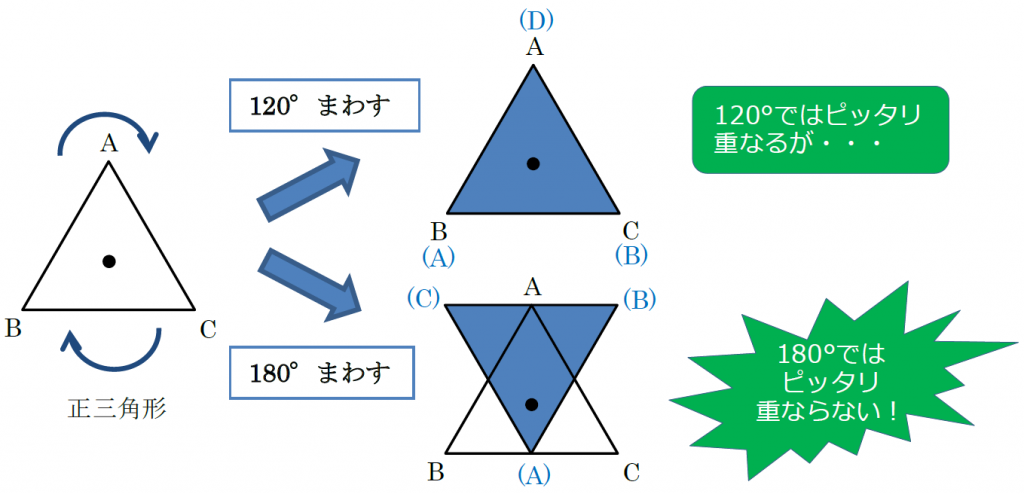
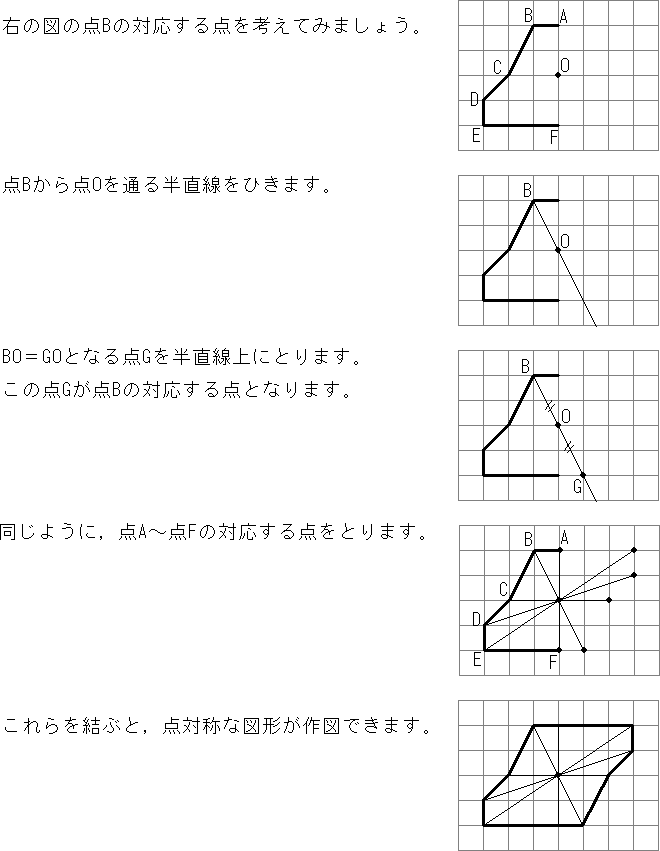
技線対称,点対称な図形をかくことができる。 知 線対称,点対称な図形の意味や性質について理解する。 関連※比較・検討場面で「考え方の関連付け」を行う場面は と示し,問題を 問 ,課題を 課 ,めあてを め ,考え方を 考 ,関連付けを 関 ,まとめを ま と示しています。点対称な図形は,線対称 な図形と違い,対称の軸 から鏡のように作図するわ けではないので注意が必 要です! 点対称な図形を作るための条件! ①対応する点を結ぶ直線は対称の中心 を通る。 ②対称の中心から対応する点までの長さ は等しくなっている。 つまり,この画像では点Aからの線対称な図形の性質は,次のようにまとめています。 点対称の定義 対称の中心のまわりに180°まわして重なる点,線,角をそれぞれ,対応する点,対応する線,対応する角といいます。 点対称な図形の性質は,次のようにまとめています。 線対称や点対称




点対称な図形のかき方2 スクールプレゼンター教材共有サイト スクプレ道場




線対称で点対称な図形をかく 算数を究める
①三角形について線対称な図形か、点対称な図形か調べよう。 直角三角形を参考に他の て表に 整理しよう。 正多角形について調べよう。 円について線対称な図形か、 点対称な図形か調べよう。 ここを折ると答えが見えません 00 00 00 00 00 Author 川口市教育委員会 Created Date①線対称・点対称の意味 ②線対称・点対称の性質 ③線対称・点対称のかき方 ④正多角形と対称な図形の見方 教え方1 折り重ねて重なる形を見せて、重ねたときの重なる点や直線に気づかせながら、線対称の図形を教えます。・ 線対称・点対称 があげられます。 このうち「線対称・点対称」は、図形問題全体に対する基礎力を養うのに格好の題材です。線対称は、鏡やガラスなど、身近なものを使えば、比較的簡単にイメージすることができますが、点描写することによって



算数の点対称のことについてです 長方形正方形ひし形正六角形正八角形二等 Yahoo 知恵袋
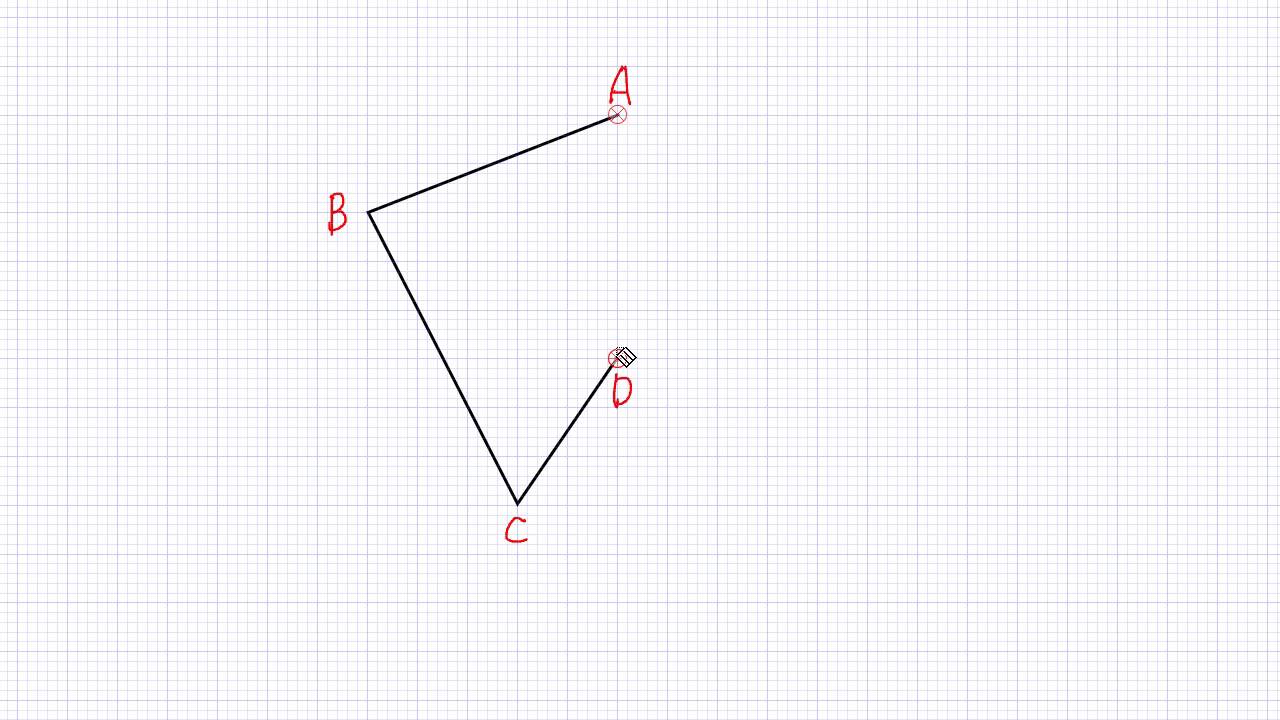



点対称な図形のかき方 Youtube
3 ・線対称な図形の性質 (考)(知)線対称な図形の性質を調べる ことができる。 4 ・線対称な図形の作図 (技)線対称の性質に基づき、線対称な 図形をかくことができる。 線対称な図形の作図コンテンツなどを 活用してかき方の理解を深める。 〔al(主)〕 デジタル教科書機能活用 ②点対称 5技 線対称な図形と点対称な図形を弁別 したり,作図したりすることができ る。 知 線対称な図形や点対称な図形の性質 を理解している。 面積を2等分 しよう ( 教p22) 14 対称軸ではない直線や折れ線で 図形の面積を2等分する。関連する学習プリント ★教科書ぴったりトレーニング コラボ教材★ 小学1~6年生 算数 確かめのテスト解説動画付き 小学6年生の算数 点対称な図形 問題プリント;
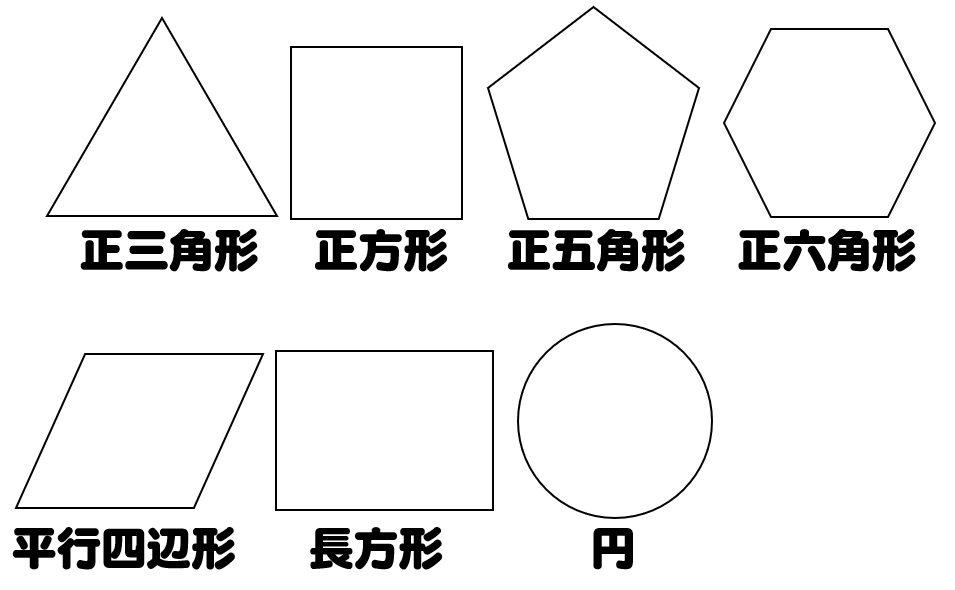



線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun
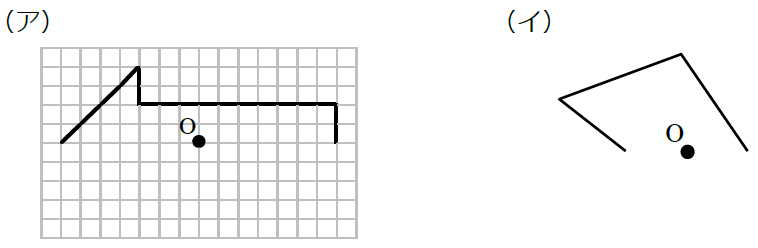



中1数学 点対称な図形とは まなビタミン
図形が線対称か、点対称かを考える 線対称の場合は対象の軸を、点対称の場合は対象の中心を描く 線対称と点対称についてまとめて 図形の、線対称と点対称について、覚えたことを確認する自主学習をしましょう。・線対称な図形の意味 ・線対称な図形の性質、作図 ・点対称な図形の意味 ・点対称な図形の性質、作図 ・四角形や三角形、正多角形などの基本図形を対称性に着目して考察すること 小学生・中学生が勉強するならスクールtv。・線対称な図形と点対称な図形の特徴を比べながら、学習を進めることができるようにするこ とが大切です。「この図形は、半分に折っても重ならないね。」「半分に切ったものを回転させ て重ねるとぴったり重なるよ。」と、前の時間の学習と関連付けている様子をほめていただ ければと
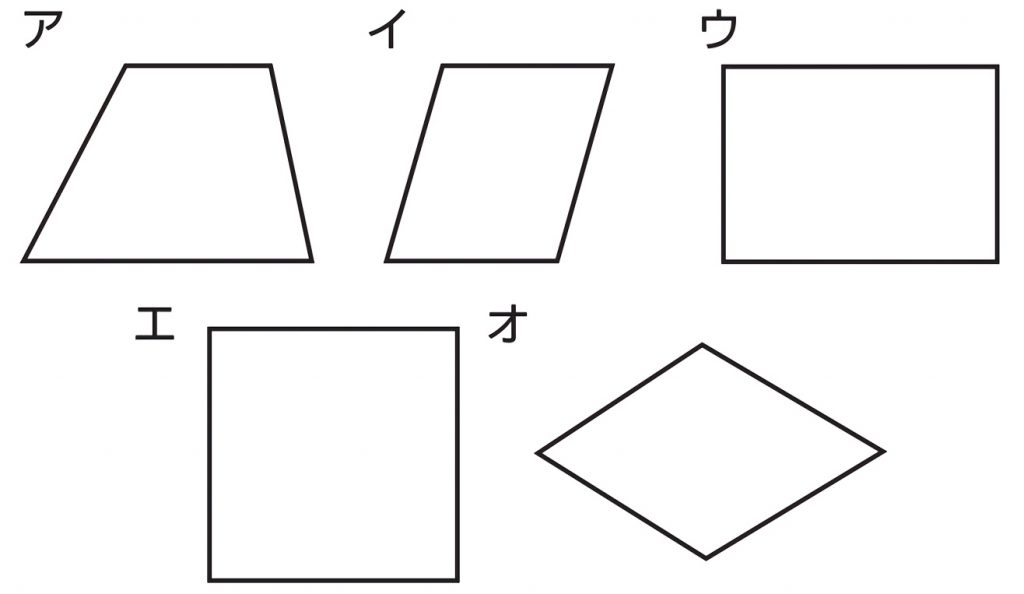



小6算数 多角形と対称 指導アイデア みんなの教育技術




大多喜町 学習支援動画 算数 小学6年生 対称な図形 線対称 点対称 Facebook
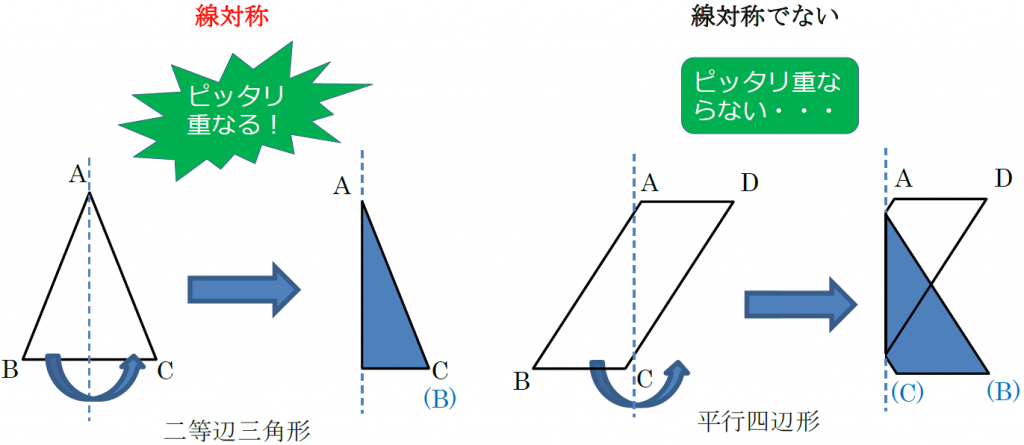
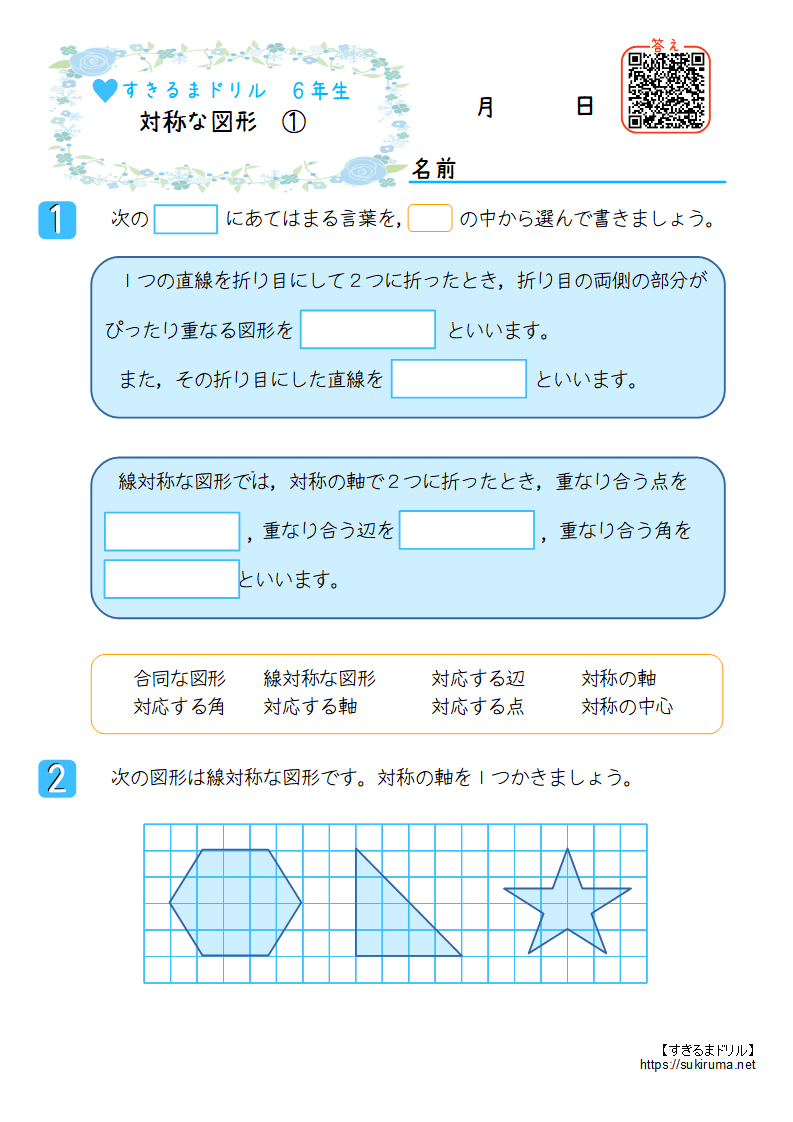
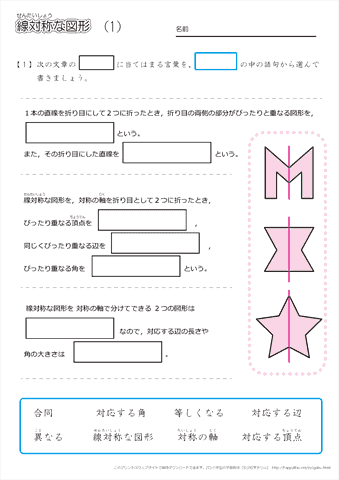
ある直線を折り目として折り返したとき,両側の図形がピッタリと重なる図形を 線対称 な図形といい,このときの直線を 対称軸 といいます。 次に,図形の線対称移動を考えます。三角形 a b c abc a bc を線対称移動させてみましょう。 まず,頂点 a, b, c a,b,c a, b, c を軸を中心に折り返して点 a ′, b ′, c ′ a',b',c' a ′, b ′, c ′ に移します。このとき, a a a と a ′ a' a ′ を結んだ線分の垂直二等分線, b b b と b ′ b' b ′ を結んだ線分の線対称な図形では,対称の軸で2つに折ったとき,重なり合う点を 重なり合う辺を 重なり合う角を といいます。 次の図形は線対称な図形です。対称の軸を1つかきましょう。 対称な図形 ① 1 , , 合同な図形 線対称な図形 対応する辺 対称の軸 対応する角 対応する軸 対応する点 対称の中心 2



Http Www Edu Tens Net Kyouikuken Kouhou Gakusyushien Pdf E6 Sansu S6 01 10ans Pdf



Search Q E7 B9 E5 Af Be E7 B0 81 E5 9b E5 E4 B8 80 E8 A6 Tbm Isch
1 対称な図形 学 年 組 氏 名 1 次の文字について,線対称な形には ,点対称な形には ,どちらでもないときは× を答えましょう。 線対称な形とは,1本の直線を折り目にして二つ折りにしたとき,両側の部分がぴったりと重なる形です。点対称な形1下の㋐~㋗の図形のうち、線対称な図形をすべて選んで記号で答えましょう。 せんたいしょう 2下の(1),(2)の図は,直線アイを対称の軸とした線対称な図形の半分です。 残りの半分をコンパスや三角定規を使ってかきましょう。 たいしょう じく じょうぎ せんたいしょう 答え ア イ振り返ろう (線対称な図形の性質と比べて点対称の性質はどうなっているかな。) (例) 線対称な図形とじで、点対称な図形も、対応する辺の長さや、角の大きさ は等しかった。対角線でなくても、対称の中心を通る直線で分けると、合になって いるのはびっくりした。どこで線を引いても
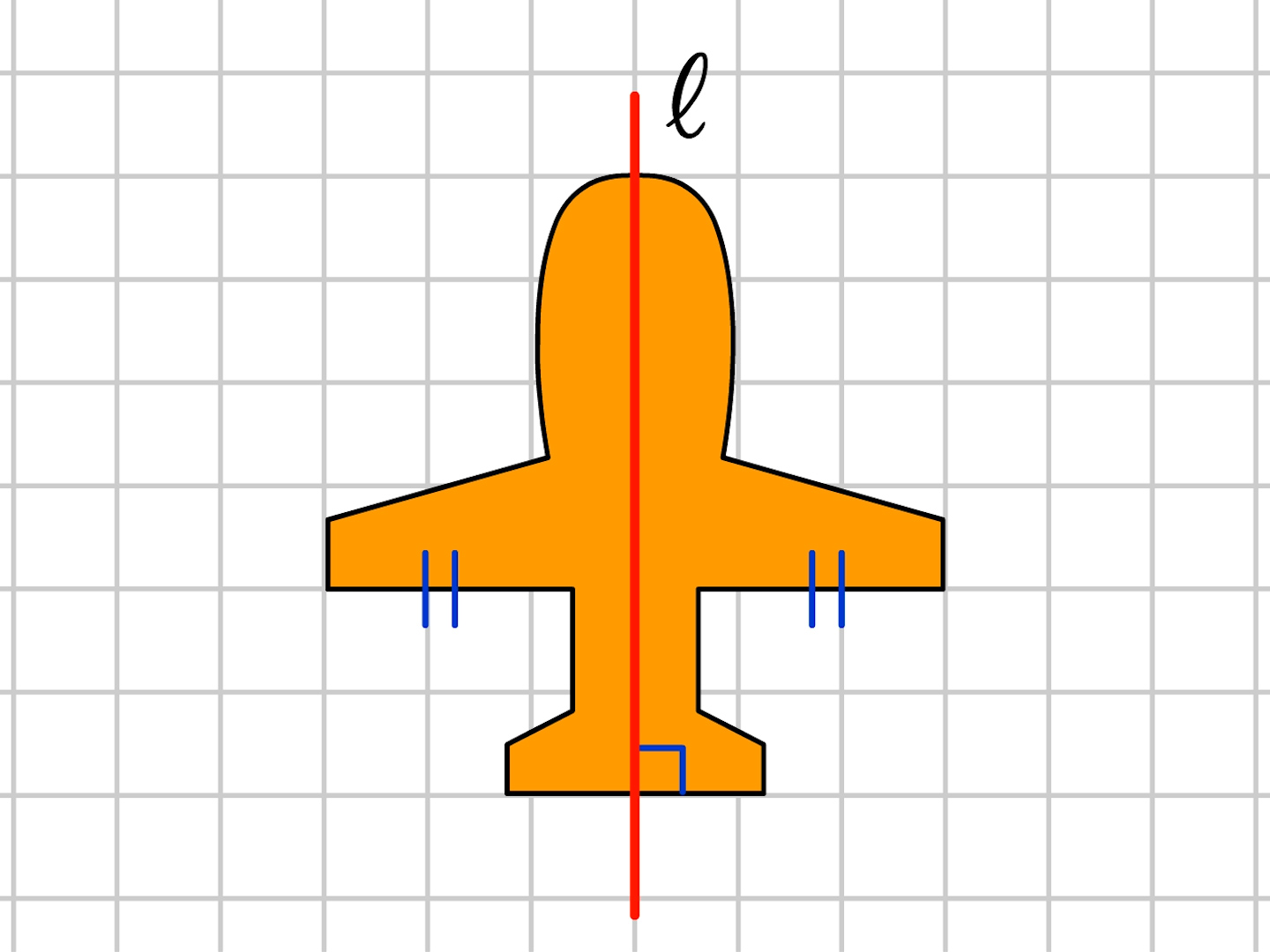



6年 線対称な図形 算数イメージ動画集 大日本図書




線対称 点対称 算数用語集
正三角形とその対称軸のうちの一本 線対称 (せんたいしょう、 英 line symmetry )は、 図形 を特徴づける性質の1つで、ある 直線 を軸として図形を 反転 させると自らと重なり合う 対称性 である。⑶ 線対称な図形であり,点対称な図形でもあるものを,すべて選びなさい。 〔 〕 2 次のことがらが正しいときには ,正しくないときには*と答えなさい。 (8点×4) ⑴ 点対称な図形では,対称の中心から対応する点までの長さは等しくなっています。 〔 〕 ⑵ 正十角形には,対称の軸が5(10点×1問) 線対称な図形を対称の軸で切ると、 な2つの形ができる。 5 下の地図記号は郵便局のマークで、線対称な図形です。対称の軸をかき入れ、 にあてはまる言葉を書きましょう。(10点×2問) 点 ①対称の軸は、どれですか。




対称な図形 F S 数学 コンテンツ




対称の授業final 算数
平面図形というと、小学生がつまずきやすいポイントとして、・ 複雑な形の面積・ 角度・ 線対称・点対称があげられます。このうち「線対称・点対称」は、図形問題全体に対する基礎力を養うのに格好の題材です。線対称は、鏡やガラスなど、身近なもの 「線対称かつ点対称な図形」には以下のいずれも該当するのだが、 各図形の個性をより厳密に表せる名称を知りたかった。 別称が存在 解決の鍵は「点対称」のほうにあった。 「点対称」の別称で「二回対称」という呼び方があることがわかった。 180度回転を2回繰り返したら図形がもと



Fdk3a7ctb5192box5b Com Es 6nen Mt Tentaishou Sakuzu Html
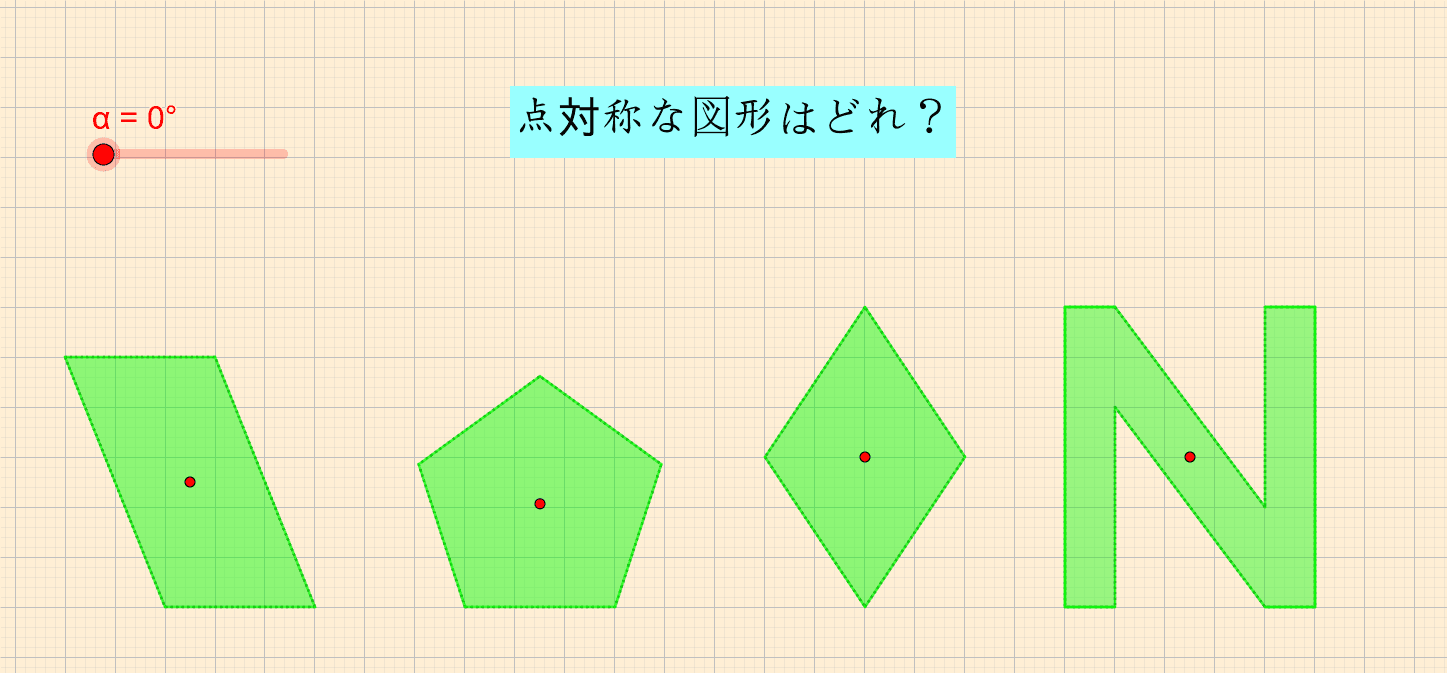



点対称な図形はどれ Geogebra



6年算数対称な図形2 正多角形教え方



点対称な図形の対応する頂点を確認する Ipadとiphoneで教師の仕事をつくる



このシンボル 県章 は線対称な図形 点対称な図形 ー6年生ー 翁島 おきなしま 小学校ホームページ




โน ตของ 対称な図形 ช น Primary算数 Clear
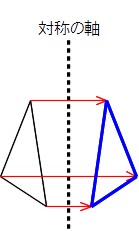



Math 点対称な図形のかき方 働きアリ
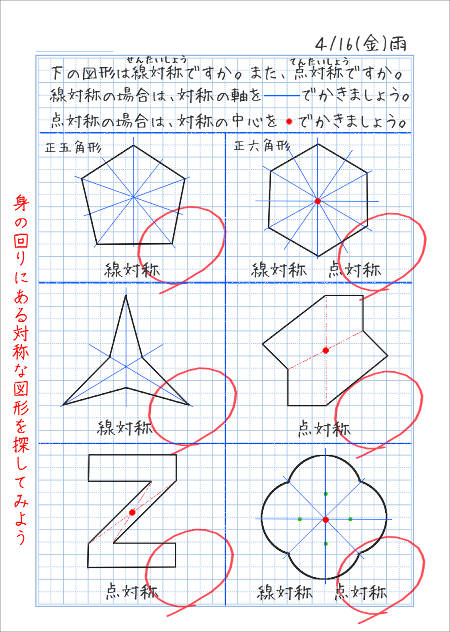



線対称と点対称の自主学習ノート 家庭学習レシピ




対称の英語 線対称 点対象 平行移動など 英語独学マスター




線対称 点対称 算数用語集



中1数学 点対称な図形とは まなビタミン
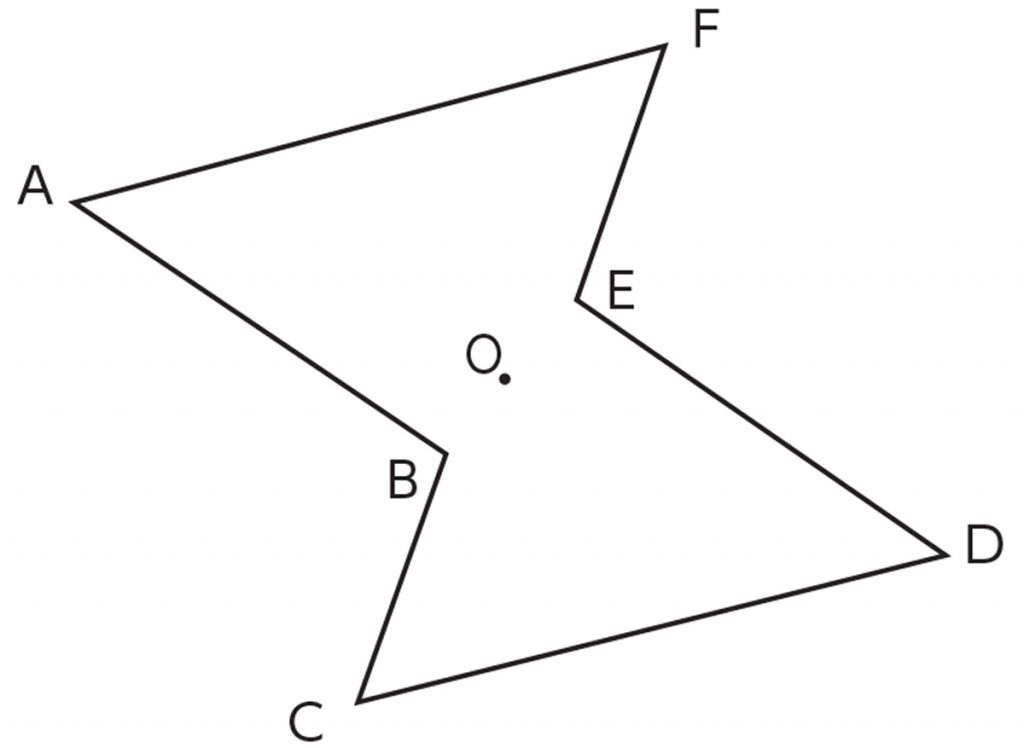



小6算数 点対称な図形の性質 指導アイデア みんなの教育技術



対称な図形 3 点対称



Studydoctor線対称 点対称な図形の書き方 中学1年数学 Studydoctor




点対称な図形はコンパスでかける 小6向けの動画です Studychannel スタディチャンネル 勉強が楽しくなる 学び 動画サービス




線対称と点対称の自主学習ノート 家庭学習レシピ
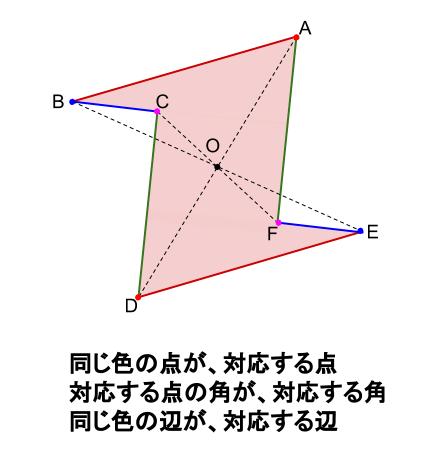



中学数学 点対称な図形 中学数学の無料オンライン学習サイトchu Su
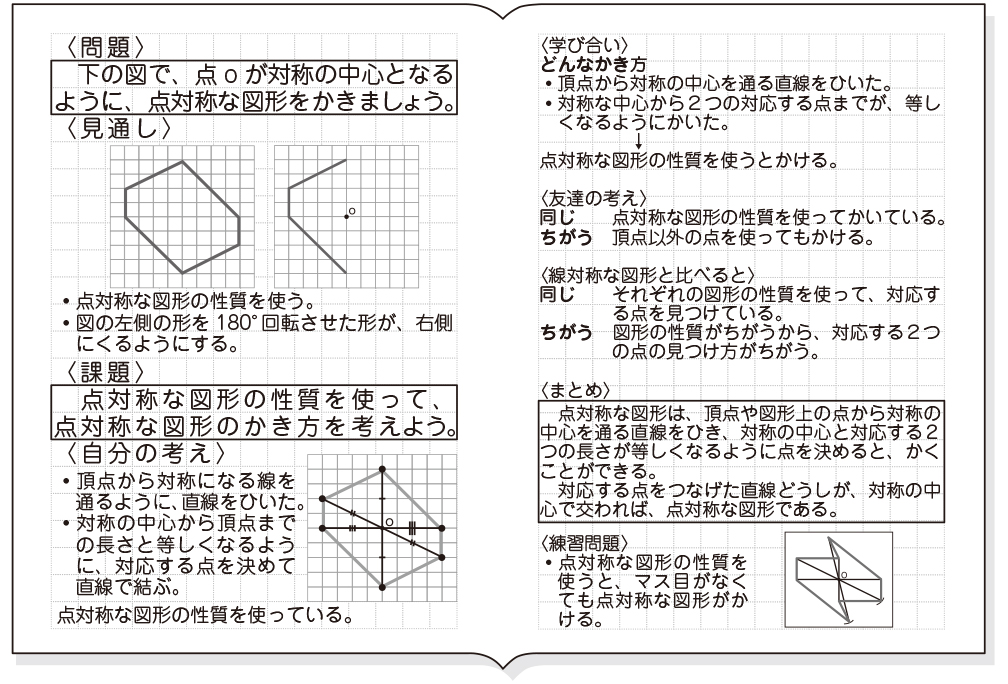



小6算数 対称な図形 点対象 指導アイデア みんなの教育技術




スマホok 6年 対称な図形 多角形と対称 Youtube



中1数学 点対称な図形とは まなビタミン




小学校算数の平面図形において 線対称 や 点対称 について習いますが これらは他の単元とは少し毛並みが異なり 独特の思考 小学校 算数 算数 正多角形




算数のヒント 2 点対称 豊富小中学校 姫路市立学校園ホームページ



対称な図形と授業運営 教育考現学



すきるまドリル 小学6年生 算数 対称な図形 無料学習プリント すきるまドリル 無料学習プリント




Square 2 Descubre Como Resolverlo En Qanda




世界一分かりやすい算数 小6 対称な図形




線対称な図形の性質 小6向けの動画です Studychannel スタディチャンネル 勉強が楽しくなる 学び 動画サービス



点対称な図形



線対称図形と点対称図形の見分け方 算数解法の極意



1



対称な図形 たしかめよう 6年生 翁島 おきなしま 小学校ホームページ



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



線対称 点対称な図形の書き方 中学1年数学 Youtube



多角形と対称 6年生 翁島 おきなしま 小学校ホームページ




線対称描画と点対称描画について Hyper Paint チュートリアル 使い方 講座




対称の中心を使わずに点対称な図形をかく 算数を究める




小学6年算数 対称な図形 活用できる教材公開 アルファベットで対称な図形を探してみよう Math Channel Note



小学校6年生iさん 身のまわりの図形と対称 の確認テストも100点 学習塾 凛 Rin 静岡県浜松市東区の個人塾



何かと教えづらい 線対称 点対称 小6 算数の教え方教えますmother S Math Happy Study Support



Fdk3a7ctb5192box5b Com Es 6nen Mt Sentaishou Sakuzu Html




6年算数対称な図形2 正多角形教え方
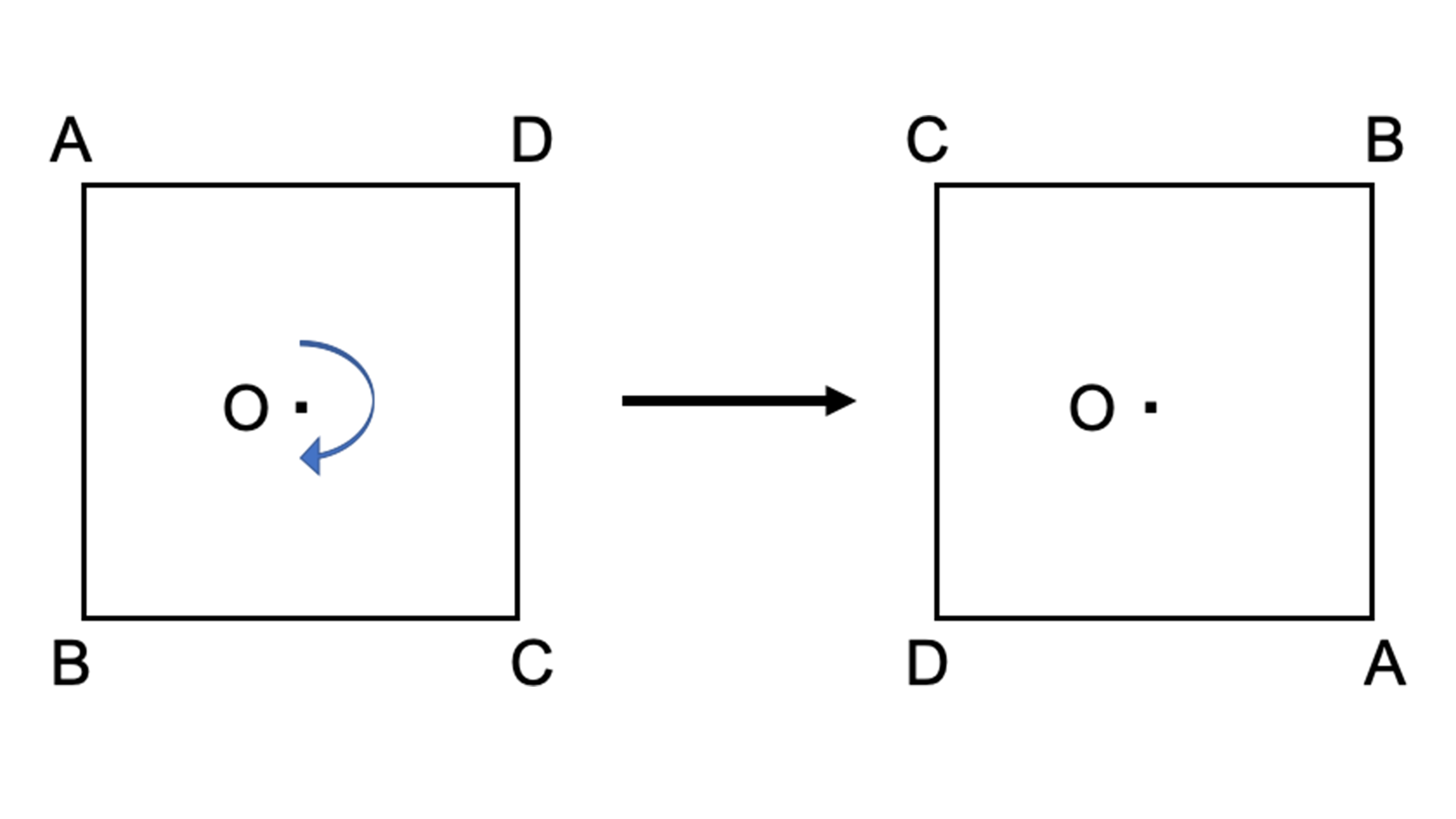



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




対称の中心を使わずに点対称な図形をかく 算数を究める
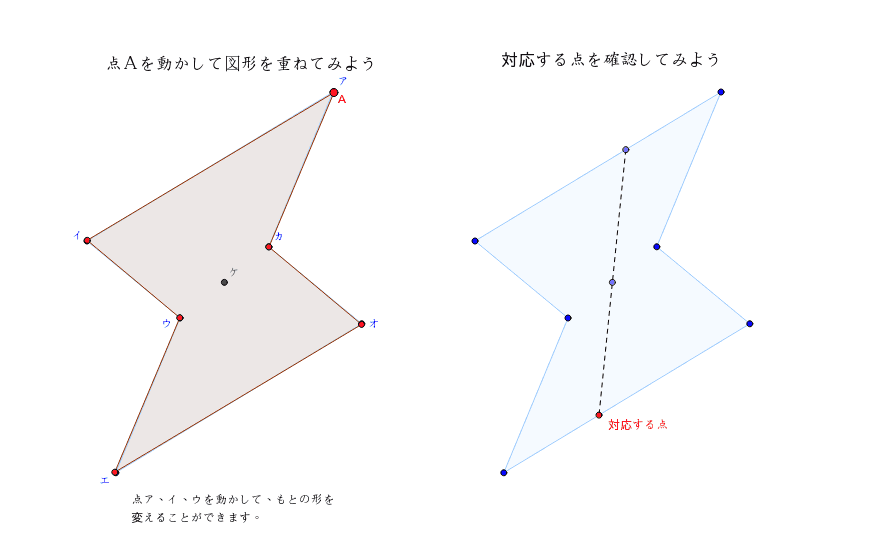



点対称な図形の観察 Geogebra
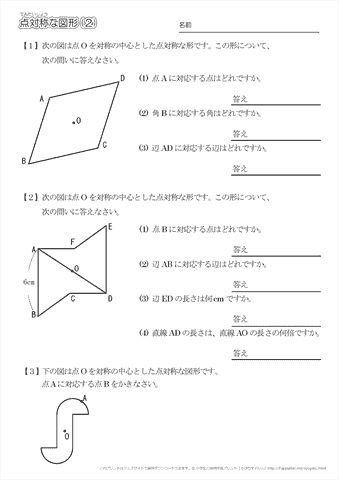



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生



線対称ではないけど点対称な図形を書け という問題で自称流行に全く興味がないという勤勉家の解答 18年02月08日の無機物のボケ ボケて Bokete
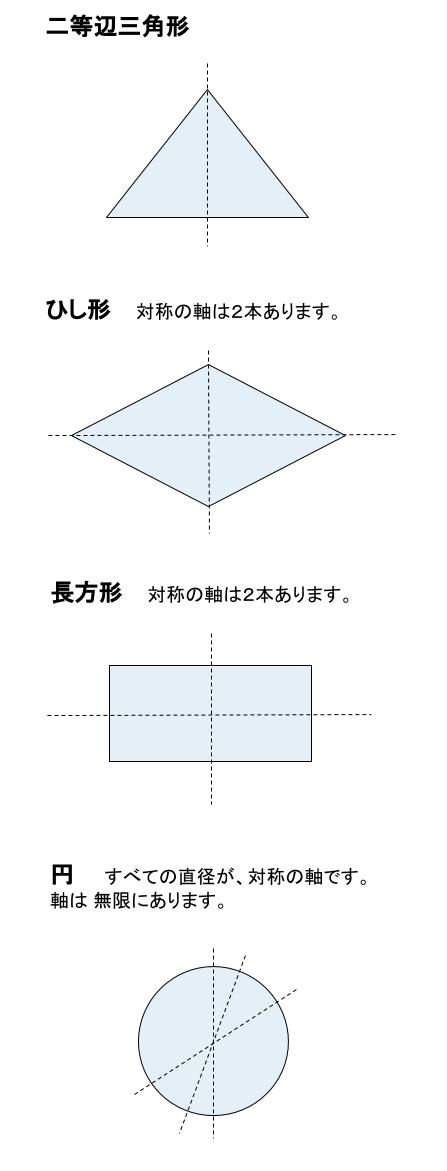



中学数学 線対称な図形 中学数学の無料オンライン学習サイトchu Su
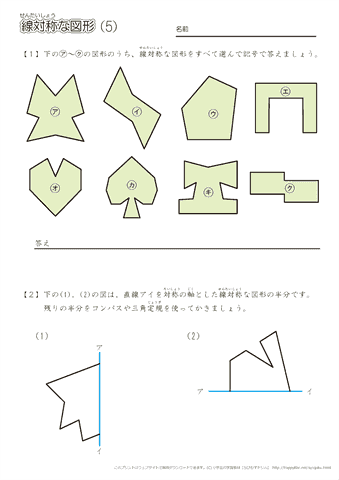



小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生



点対称な図形
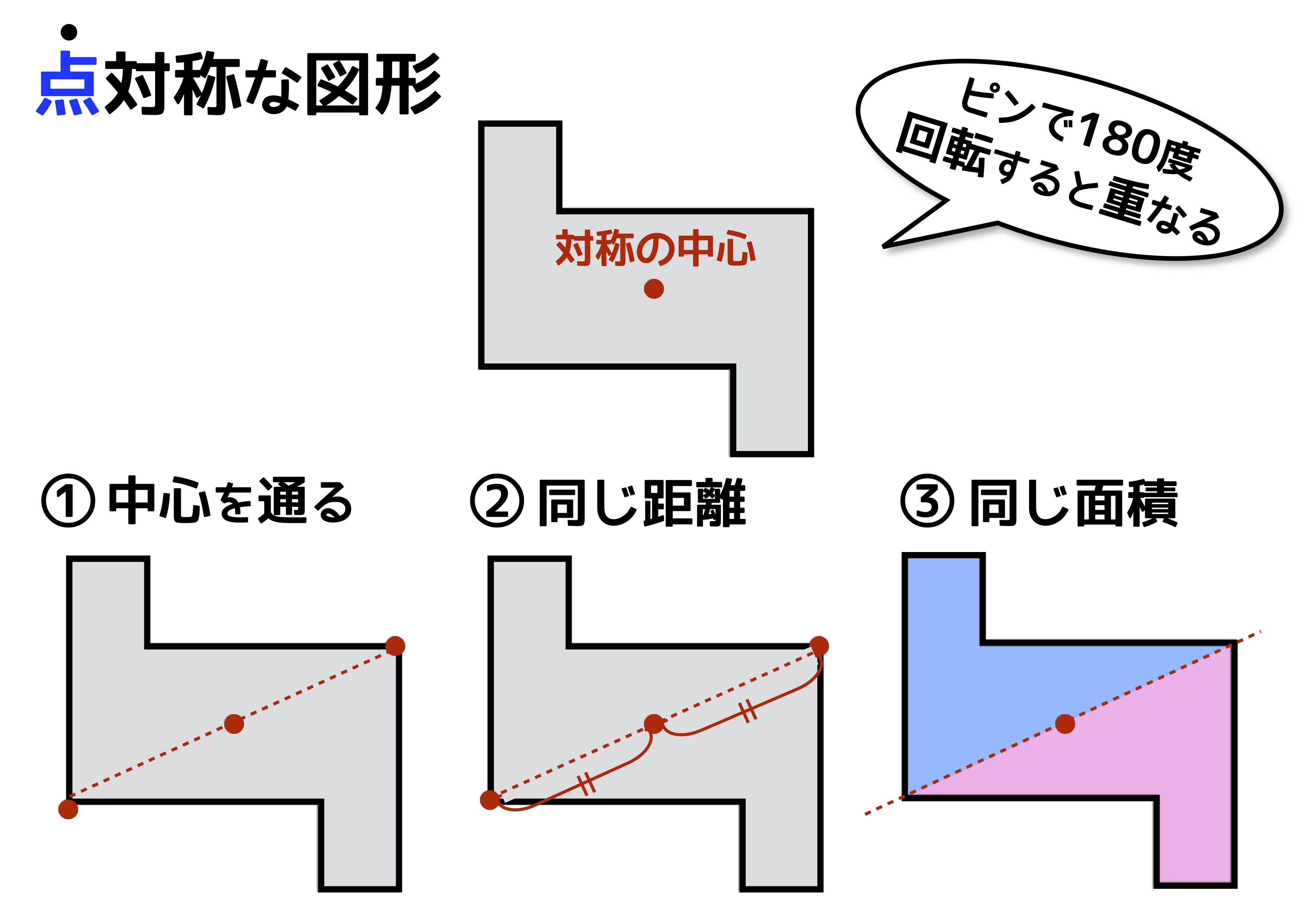



線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ



Www Shinjuku Ed Jp Es Tsukudo 91 Pdf
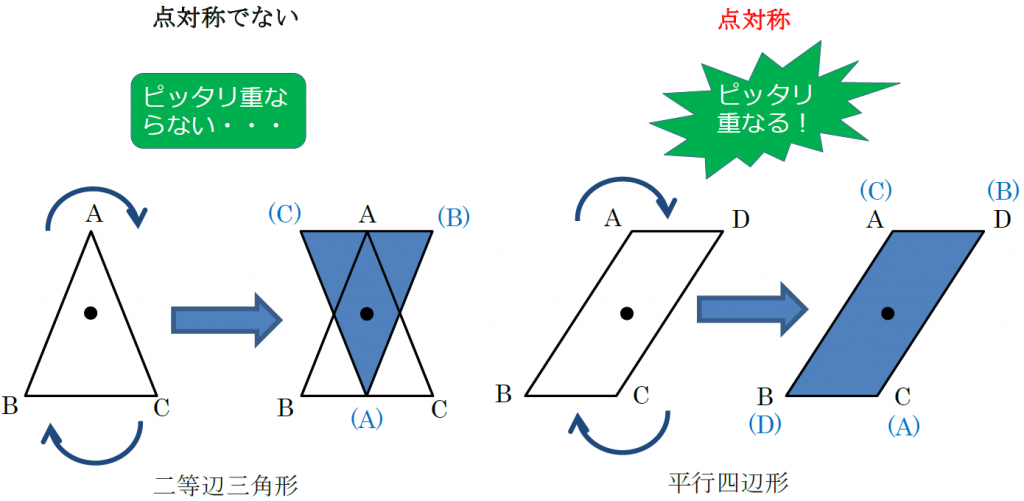



中1数学 点対称な図形とは まなビタミン




小6 対称な図形 四角形 日本語版 Youtube




世界一分かりやすい算数 小6 対称な図形




スマホok 6年 対称な図形 算数をつかってやってみよう 線対称や点対称な図形をかいてみよう Youtube
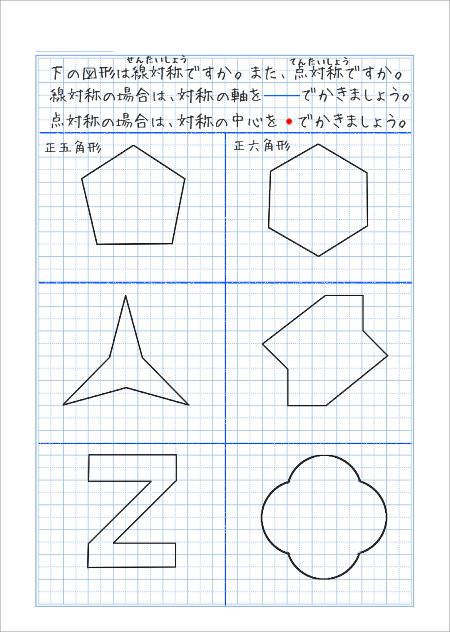



線対称と点対称の自主学習ノート 家庭学習レシピ
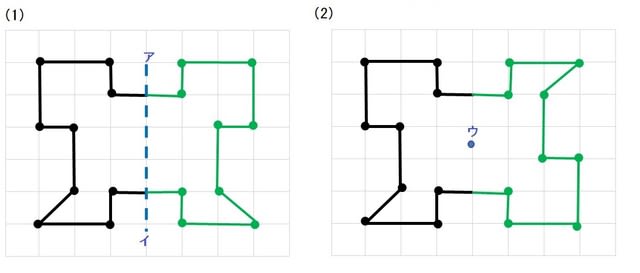



何かと教えづらい 線対称 点対称 小6 算数の教え方教えますmother S Math Happy Study Support




6年算数 対称な図形 9時間目 いろいろな図形を対称の見方で調べよう Youtube




線対称 点対称な図形のかき方 対称な図形 小6算数 豊橋の学習塾 勉強 Youtube スタディチューブ




悩みのタネ 解決編 線対称と点対称 声に出さないけど思っていること



6年算数線対称点対称図形 わかる教え方




線対称 点対称とは 具体例6選と応用問題3選で解説します 遊ぶ数学



Math 点対称な図形のかき方 働きアリ



何かと教えづらい 線対称 点対称 小6 算数の教え方教えますmother S Math Happy Study Support



1



1




点対称の図形の書き方を教えてください Clear



Www Pref Saitama Lg Jp Documents R2suugaku7b Pdf
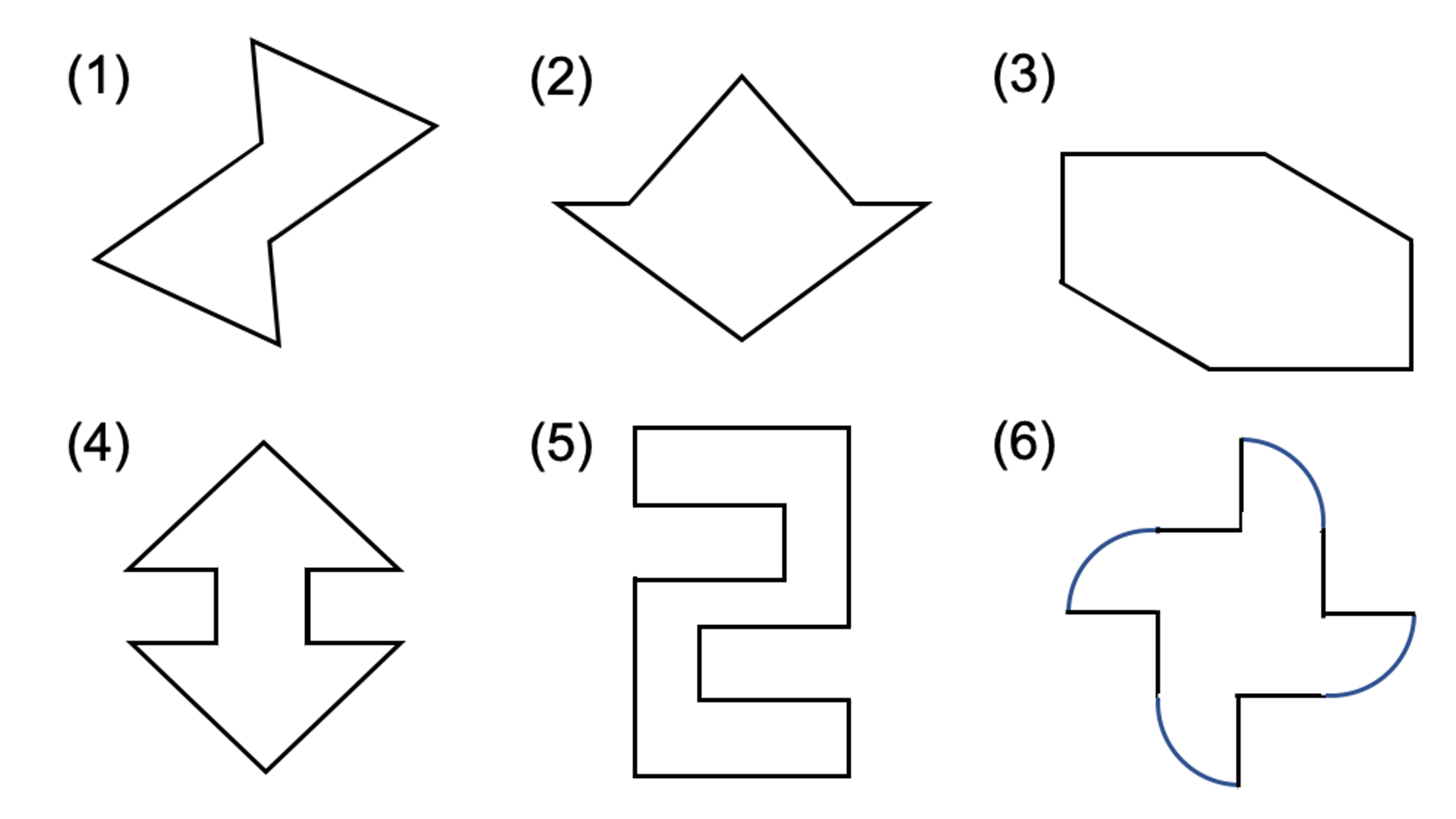



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



多角形と対称 6年生 翁島 おきなしま 小学校ホームページ
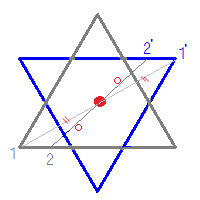



線対称 点対称




対称な図形 Ict教材eboard イーボード



小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生




対称な図形 線対称と点対称 小学生 算数のノート Clear



線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ




3x5 Left 2times 5rig Descubre Como Resolverlo En Qanda



アルファベットのa H R Zの中で 点対称な図形と線対称な図形 線対 Yahoo 知恵袋



高校入試 英語 数学 学習 線対称と点対称




線対称な図形を書く



点対称な図形のかき方 中学数学 定期テスト対策 ベネッセ教育情報サイト




小六の復習 線対称 点対称な図形 小学生 算数のノート Clear



小6算数 多角形と対称 指導アイデア みんなの教育技術
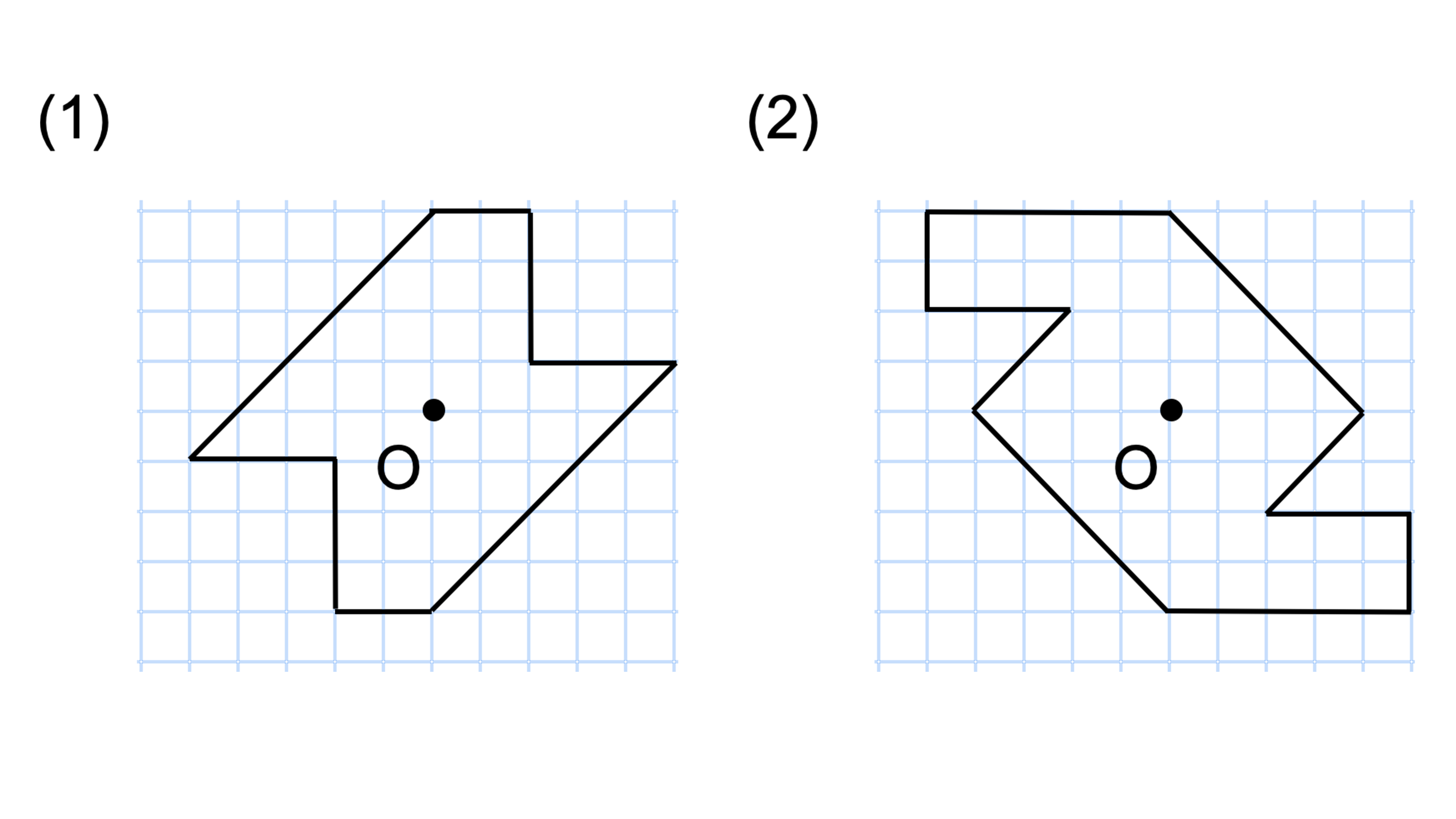



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
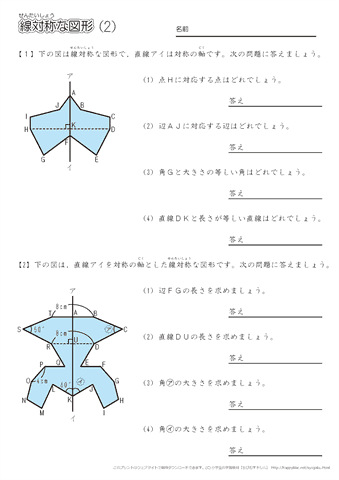



小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生




世界一分かりやすい算数 小6 対称な図形
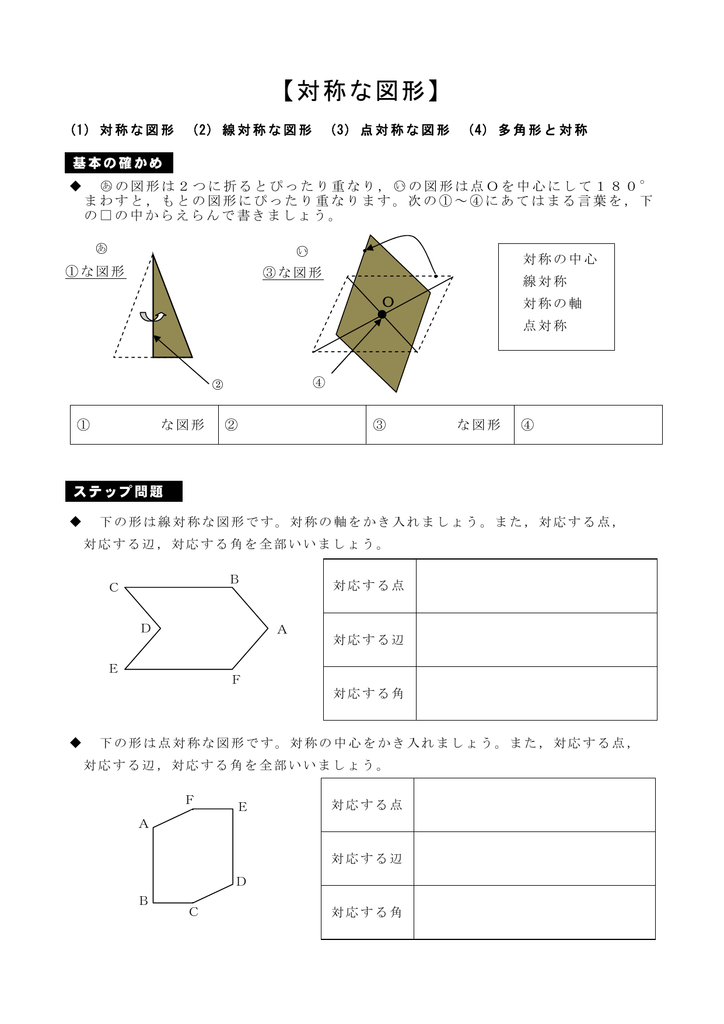



対称な図形



0 件のコメント:
コメントを投稿