展開(多項式の乗法3) 1次の式を計算しなさい 練習問題は印刷してプリントとして使えるものから、pcやスマホから直接できるものまであり、普段の予習復習や定期テスト対策、受験勉強まで中学生の学習を強力にサポートします。6 L T 62 = T E = 6の展開 z T E = ;L T 6 F = 6の展開 zいろいろな式の展開 z素因数分解、因数分解

中学3年生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
多項式の展開 問題
多項式の展開 問題-T F = ;単項式×多項式の式の展開4の演習問題です。 ちなみに、 単項式×多項式の式の展開4 に一覧があります。 下記のページには、つぎのような単項式×多項式の式の展開4の演習問題が10問あります。 多項式は2項、変数は1文字、定数あり、乗数ありです。 1 8x




中学3年生 数学 多項式の乗法と除法 式の展開 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
多項式 例題 多項式と単項式の乗法除法 式の展開 乗法公式(xa)(xb)の展開 乗法公式 2乗の展開 乗法公式 和と差の積の展開 式の展開 いろいろな計算 式の展開 四則 因数分解1_共通因数をくくりだす 因数分解2_(xa)(xb) 因数分解3_2乗 因数分解4_(xa)(xa) 因数分解 おきかえ 共通因数をくくりだした後通常,式の展開は次のような順序で,「総当たりで」掛けると考えることが多いが,二項定理,多項定理の解説はこの方法では分かりにくいので,「代表選手の選び方」で解説してみる. 右図のように各々の( )からどちらか1つの項 a , b を選んで中3 多項式の計算 展開 練習問題⑧ 中3 多項式の計算 展開 練習問題⑧ 今回の問題はこちら 解説は下にあります。 解説はこちら 中学数学の解法辞典 184 subscribers Subscribe
多項式の積の展開がわからない方は、こちらのページを見てみてください! →中3数学多項式を展開するときの4つの便利な公式を覚えよう! 次の式を因数分解してみよう。 \(xy4y=(x4)y\) 多項式の計算 展開 文章題② 今回の問題はこちら 縦の長さがacmで、横の長さが縦の長さより2cm長い長方形Aがあります。T E > ;の展開 z T E = ;
多項式と単項式の乗法と除法 単項式に多項式をかける乗法は、分配法則を使ってかっこを外して計算する。 1 次の計算をしなさい。 a (bc)= ab ac ( a b )÷c =( a b )× = 多項式を単項式でわる除法は、わる式の逆数をかけて計算する。関連練習問題 Lesson1 多項式と単項式の乗法と除法 Lesson3 式の展開(2) ‐ 乗法公式1 Lesson4 式の展開(3) ‐ 乗法公式2 Lesson5 因数分解(1) ‐ 素因数分解 Lesson6 因数分解(2) ‐ 乗法公式の利用1 Lesson7 因数分解(3) ‐ 乗法公式の利用2 Lesson8 式の展開 多項式:問題1 次の中から多項式を全て選べ。 4xy、3x2y、53a、x 2 4y 2 z 解答&解説 多項式は、3x2y、53a、x 2 4y 2 zの3つです。 多項式:問題2 多項式4x 2 yz 3 y 4 z8y 3 z 4 の次数を求めよ。 解答&解説 多項式の次数を求めるには、各項に文字が何個掛け




中学数学3年 単項式と多項式の乗法と除法 受験の月
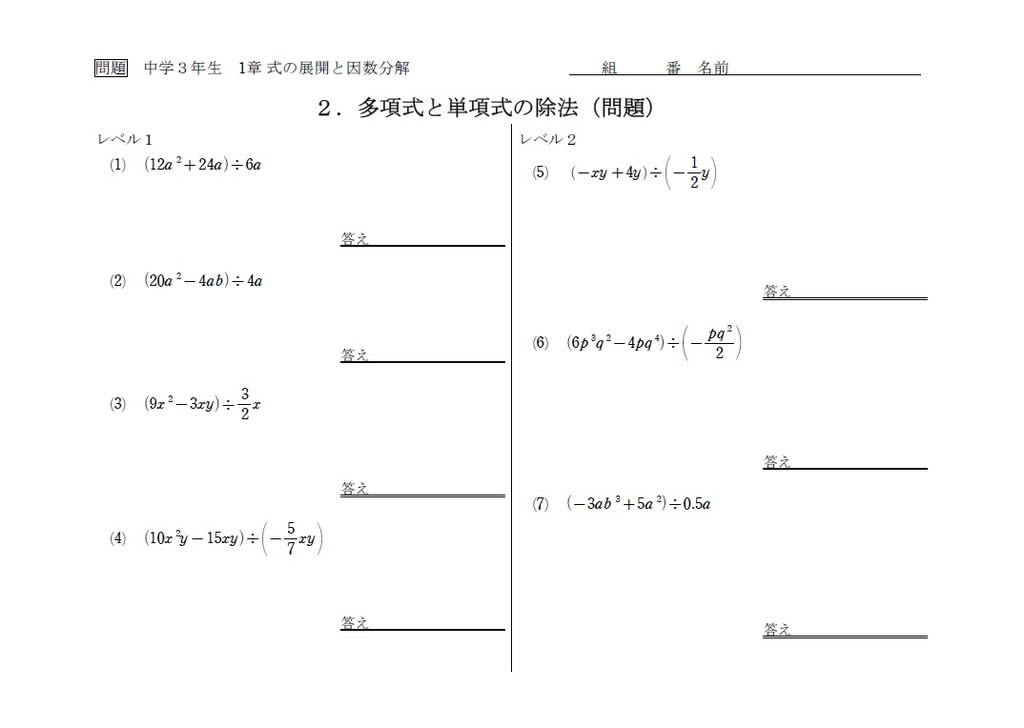



中3 展開と因数分解2 動画 練習プリント レベル2の解説 中学数学の勉強に
高校数学の基本問題 Gogle site →数ⅠA →数ⅡB →数Ⅲ (旧C) ***最近の更新*** 反復試行の確率(入試問題) 絶対値付き関数の定積分 Rの関数hist () Rの関数sample () 名義尺度データの比率の検定 フィッシャーの正確コロキウム室 (お祝い問題・多項式展開係数) この度のドメイン取得により、新しいホームページのオープン 誠におめでとうございます。 これからの貴ページの益々の発展と 管理者のご活躍を心から、お祈りします。 ここで、お祝いの印しに多項式 例題 多項式と単項式の乗法除法 式の展開 乗法公式(xa)(xb)の展開 乗法公式 2乗の展開 乗法公式 和と差の積の展開 式の展開 いろいろな計算 式の展開 四則 因数分解1_共通因数をくくりだす 因数分解2_(xa)(xb) 因数分解3_2乗 因数分解4_(xa)(xa) 因数分解 おきかえ 共通因数をくくりだした後




中3数学の基本問題プリント 問題と解答



数と式の問題 Of 京極一樹の数学塾会員頁
サンプル&サンプル的なもの紹介 今回作成&アップロードしたプリントは、単項式×多項式、多項式×単項式、多項式÷単項式、多項式×多項式の計算問題をまとめたものです。以下の記事で載せた問題を元にしたものになっています。 ※式の展開問題編(無料note)↑ この中の問題多項式 展開_ 例題と練習 2年 連立方程式 解と係数 (1)問題, (3)答b=5(誤) b=3(正) 1年 文字式の計算2(加減)3③答 17 a → − 17 a 2年 角度2 3③130°→131° 3年 放物線と図形1 5(3)解答(0,4)→(0,4)または(0,4) 多項式と単項式の乗除 基本的な式の展開の練習問題プリントです。 正確に計算出来るように練習してください。 *画像をクリックするとpdfファイルをダウンロード出来ます。 単項式と多項式の乗除 順番に計算します。 分数の割り算は逆数にしてかけ算に




世界一わかりやすい数学問題集中3 1章 式の展開と因数分解



数と式の計算問題 まずは公式をしっかり覚えよう 三重の個人契約家庭教師
ソフト名: 多項式の展開問題作成ソフト 10 ファイル: tenkaiexe / 41,448Bytes / 式と証明|多項定理について 今回は、多項定理について学習しましょう。 二項定理と同じように、多項定理も式の展開に関する定理です。 この定理を利用すれば、展開後の式を求めることができます。 どちらかと言うと、展開式を求める問題ではなくテイラー多項式の次数を上げていったとき収束するか否か,つまりテイラー展開が存在するかどうかは少々難しい問題です。 また,変数 \(x\) がある範囲にあるときは収束する,というような場合もあり




乗法公式 無料で使える中学学習プリント




中学数学 式の展開の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
〜今回のテーマ〜 多項式の分配法則や乗法の公式等、展開のやり方を覚えよう。 その他の単元や計算問題はこちら ↓ ↓ ↓ はじめに このシリーズでは、各教科・各単元に登場する基本事項(用語やその定義、公式等)を中心にまとめていきます。 現役中学生・高校生の軽い予習・復習6 L T 62 = T E = 6の展開 z T F = ;第6 回解答:その1 3 ことをテイラー展開と呼びます1。(aのことを「展開の中心」と言います。)また、定義域内の任 意のaにおいてテイラー展開可能な関数を解析関数とか実解析的関数と呼びます。この用語を使 うと、前回の演習はC∞ 級関数はすべて解析関数であると仮定した(あるいは




多項式の加減法の応用問題 かっこの前がマイナスの問題がよく出る 中学や高校の数学の計算問題




多項式の計算 清水塾
ラゲール多項式と陪多項式の注意 おもに、ラゲール多項式 とラゲール陪多項式 について学ぶ。 の肩に があるかどうか注意しておく。 ただし、 の関係は一応ある。 の有無は、微分方程式の中に が入っているかどうかでわかる。 以下では、微分方程式とラゲール多項式について簡単にまとめた。 中3数学「多項式」のさいごは、式の計算の利用を解説します。 式の計算の利用には、5種類の問題があります。 展開を利用した計算 (例: 52^2 を工夫して計算せよ) 因数分解を利用した計算 (例: 29^2 21^2 を工夫して計算せよ) 式の値 (例: x=96 のをf のaにおけるn次のテイラー近似多項式と呼ぶことにします。 問題2 問題1 をテイラー近似多項式を使って計算せよ。 問題3 f(x) = esinx cosxの0 における6 次のテイラー近似多項式を計算せよ。 問題4 極限 lim x→0 (1x)1x −e(abx) x2 が存在するためのa, bの値と
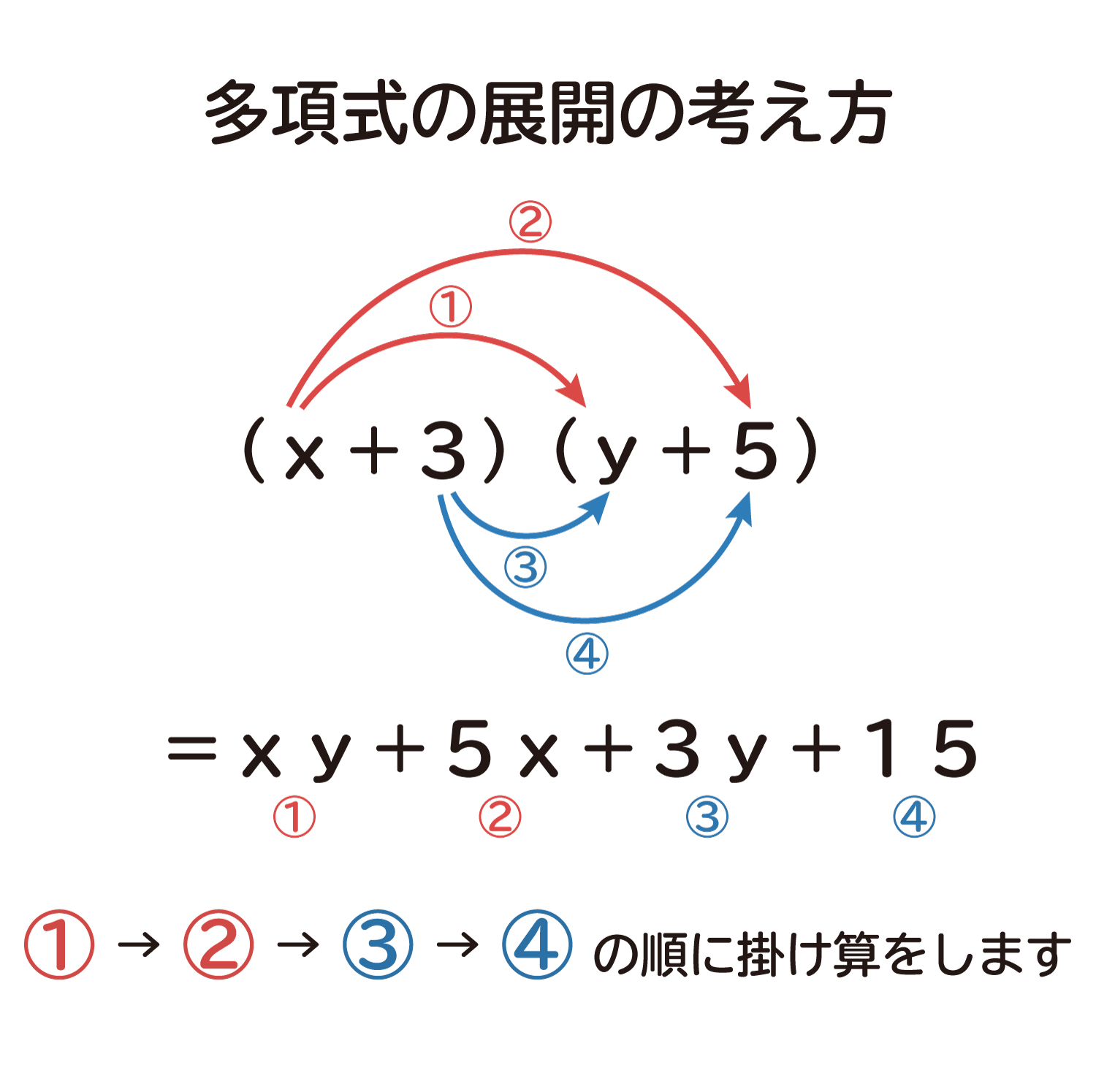



多項式同士の掛け算の展開の考え方 おかわりドリル



U9j580gf8iba369ji2w Xyz P 565
展開 (基本問題1) 1 次の式を展開せよ。 ① a (x2) ② x (x3) ③ x (x5) ④ (4x 212)÷2 ⑤ (3x 2 9x12)÷3 2 次の式を展開せよ。 ① (x2) (x5) ② (x3) (x1) ③ (x9) (x11) ④ (x4) (x3)多項式の展開問題作成ソフト ソフトのバージョン あなたの名前 (※) (ハンドル可) OSのバージョン (※) Windows 8 モード (※) 32bit版 64bit版 WOW64(64bit版エミュレーション) 動作状況 (※) 動作した 条件付きで動作 動作不可、インストール不可 詳細情報また、直交多項式の積分の範囲が有限であるチェビシェフ多項式やルジャンドル多項式は大学入試の数学問題にも出やすいが、 ラゲール多項式は積分範囲が 0 から `oo` なので、大学入試の試験問題で出ることはまずないだろう。 さて、ラゲール多項式の




中3 展開と因数分解3 多項式と単項式のいろいろな計算 予習 中学数学の勉強に




中3 展開と因数分解1 多項式と単項式の乗法 予習 中学数学の勉強に
展開(単項式と多項式の乗除2) 1 次の式を計算しなさい 練習問題は印刷してプリントとして使えるものから、pcやスマホから直接できるものまであり、普段の予習復習や定期テスト対策、受験勉強まで中学生の学習を強力にサポートします。中学3年生 数学 多項式の乗法と除法・式の展開 問題プリント 無料ダウンロード・印刷 中学3年生数学「多項式の乗法と除法・式の展開」の問題を繰り返し練習できる教材プリントを無料ダウンロード・印刷できます。多項式 例題 多項式と単項式の乗法除法 式の展開 乗法公式(xa)(xb)の展開 乗法公式 2乗の展開 乗法公式 和と差の積の展開 式の展開 いろいろな計算 式の展開 四則 因数分解1_共通因数をくくりだす 因数分解2_(xa)(xb) 因数分解3_2乗 因数分解4_(xa)(xa) 因数分解 おきかえ 共通因数をくくりだした後




展開 因数分解の利用 図形 清水塾




中学3年数学 3項式の展開 Youtube
中学数学 多項式の問題 z多項式の計算 z多項式と単項式の乗除 z多項式と多項式の乗法 z T E = ;数学31章式の展開と因数分解「多項式の乗法」<応用問題②・解答> 4つの数の組の,左上の数に注目する。 かけられる数(たての数)をm,かける数(横の数)をn とすると,左上の数はmnと表せる。 mn m(n+1) 左下の数は(m+1)n




数学 多項式の係数を求める問題 展開 大学入試数学の考え方と解法




中学3年生 数学 多項式の乗法と除法 式の展開 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中3数学の計算問題プリント 式の展開 桜花 現役バイト塾講師 Note




中3数学の計算問題プリント 式の展開 桜花 現役バイト塾講師 Note



U9j580gf8iba369ji2w Xyz P 565




中学3年生 数学 多項式の乗法と除法 式の展開 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
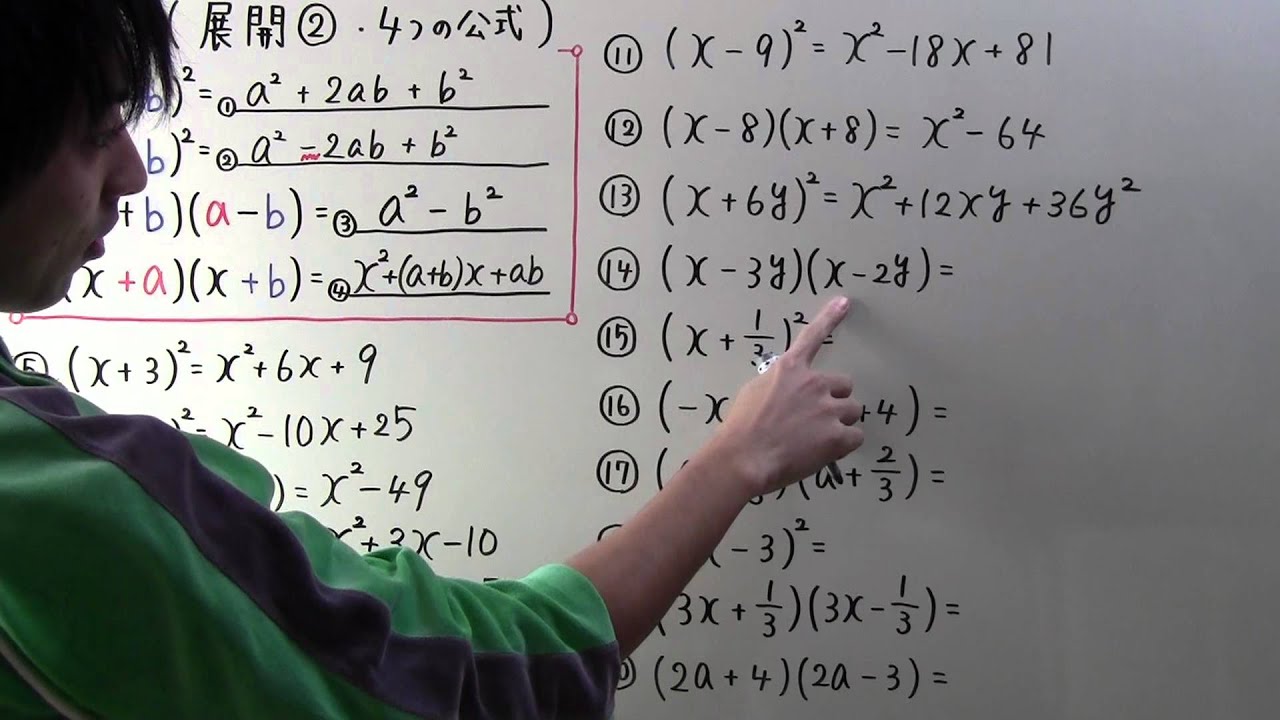



数学 中3 3 展開 4つの公式 Youtube




多項式の計算 第1講 例題解説 清水塾



数と式の問題 Of 京極一樹の数学塾会員頁




國三 Junior High数学的数学 多項式と単項式の乗除 式の展開 筆記 Clear



中学3年数学 式の展開と因数分解 多項式の計算 練習問題10 あんのん塾



Studydoctor分配法則による多項式の展開 中3数学 Studydoctor




中2数学の発展問題プリント 問題と解答




三乗の展開公式 A B 3乗の計算方法は 問題を使って解説 数スタ




中学数学 多項式 の教え方 展開の応用問題




世界一わかりやすい数学問題集中3 1章 式の展開と因数分解




中学数学 式の展開 因数分解



数と式の問題 京極一樹の数学塾




展開 因数分解を利用した計算の工夫 無料で使える中学学習プリント




中学3年生 数学 多項式の乗法と除法 式の展開 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
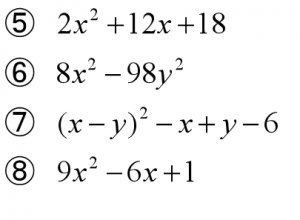



因数分解に慣れよう 後編 インターネット家庭教師のアスミラ




多項式と単項式の乗除 無料で使える中学学習プリント




数学 A B C 二乗の展開公式は 問題の解き方は徹底解説 数スタ




中3 数学 多項式の計算 よくあるミス 中学生 数学のノート Clear



1




中学3年生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




多項式の計算 清水塾
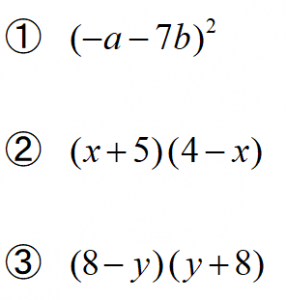



いろいろな多項式を展開してみよう 前編 インターネット家庭教師のアスミラ




数学単元別シリーズの販売 教材出版 学林舎




中学数学 多項式 の教え方 展開の基本




中学数学 多項式と多項式の乗除 中学数学の無料オンライン学習サイトchu Su




中3数学 展開の公式のやり方は 問題を使って徹底解説 数スタ




モノマナビ研究所



1
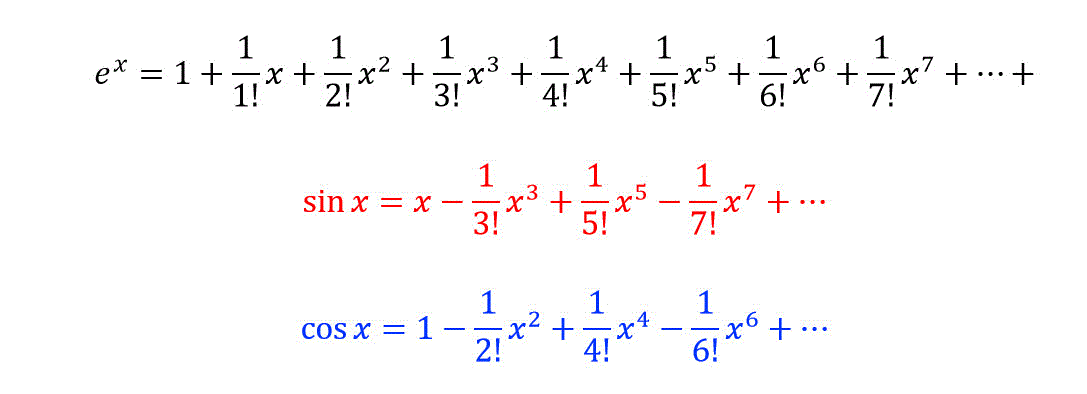



うさぎでもわかる解析 Part04 マクローリン展開 テイラー展開 工業大学生ももやまのうさぎ塾




4つの乗法公式 教遊者




中学数学 多項式 の教え方 展開の応用問題




中3 展開と因数分解3 多項式と単項式のいろいろな計算 予習 中学数学の勉強に
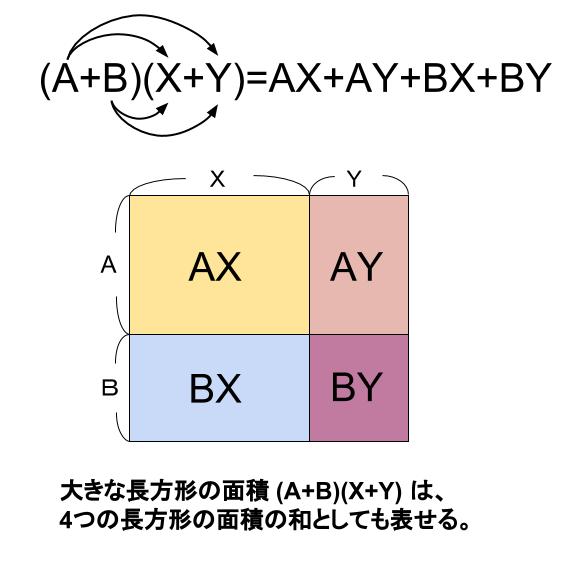



中学数学 多項式と多項式の乗除 中学数学の無料オンライン学習サイトchu Su




中学3年数学 式の展開と因数分解 多項式の計算 練習問題9 あんのん塾
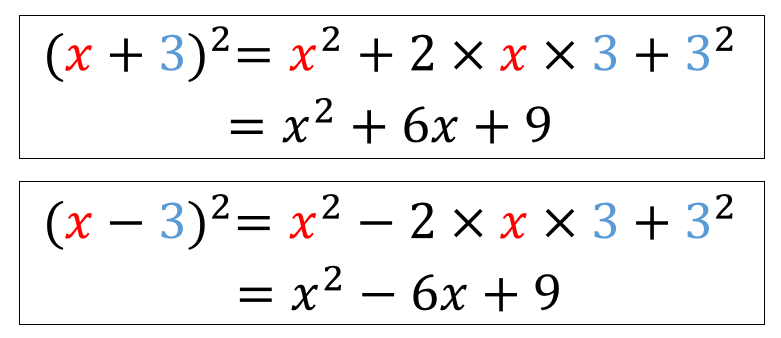



中3数学 展開の公式のやり方は 問題を使って徹底解説 数スタ
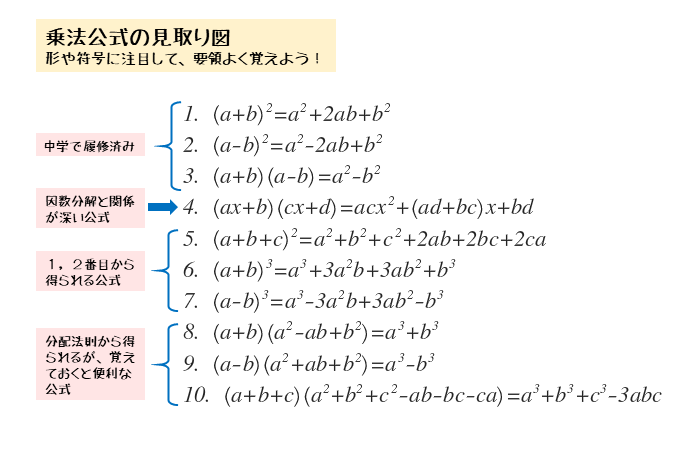



数と式 整式の展開に関する問題を解いてみよう 日々是鍛錬 ひびこれたんれん




中学3年数学 式の展開と因数分解 多項式の計算 2確認問題1 あんのん塾
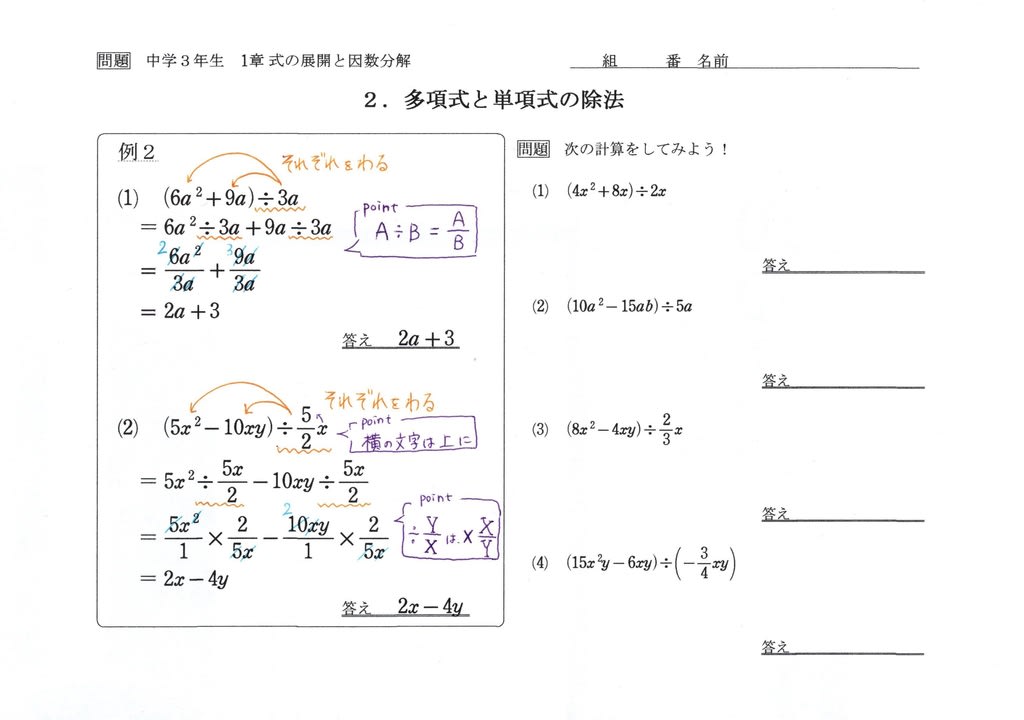



中3 展開と因数分解2 多項式と単項式の除法 予習 中学数学の勉強に




中学3年数学講座第1章3多項式 多項式応用問題解説 Youtube




式の展開と因数分解 の問題のわからないを5分で解決 映像授業のtry It トライイット




展開公式のまとめ 中学生や高校生の子はぜひ覚えておきたい 中学や高校の数学の計算問題




中学数学3年 展開と乗法公式 受験の月




中3 展開と因数分解2 多項式と単項式の除法 予習 中学数学の勉強に



数学 展開 公式 数学の展開問題 解き方のコツ 公式 スタディサプリ大学受験講座 Www Ourfuture Qld Gov Au




中学3年生 数学 多項式の乗法と除法 式の展開 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Www Hokkyodai Ac Jp Images Info Topics Pdf




中学2年生 数学 式の計算 多項式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中3数学の計算問題プリント 式の展開 桜花 現役バイト塾講師 Note




式の展開




中学数学 式の展開 因数分解



Sukinakazu Net Takousiki Takousiki Pdf



3 7第1章多項式 乗法公式 いろいろな式の展開




中学3年数学 式の展開と因数分解 多項式の計算 練習問題4 あんのん塾




中3 展開と因数分解4 多項式の乗法 予習 中学数学の勉強に




多項式と単項式の乗除 無料で使える中学学習プリント




高校数学 展開のおさらい1 例題編 映像授業のtry It トライイット




この問題教えてください 全然わかりません Clear




中学3年生 数学 多項式の乗法と除法 式の展開 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
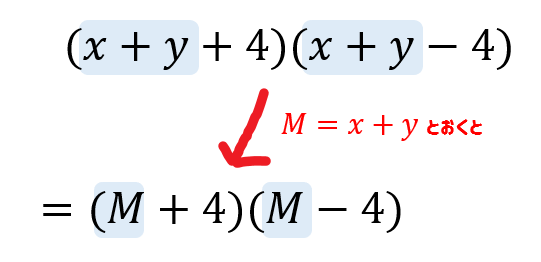



高校数学 式の展開の工夫 置き換えや組み合わせを利用するやり方を解説 数スタ




中学3年 数学の世界3 多項式の計算と式の展開 教科書予習復習練習問題 赤城 ᐡᐤᐡ




中3数学 単項式 多項式の乗法 練習編 映像授業のtry It トライイット



U9j580gf8iba369ji2w Xyz P 608




高校数学 多項定理 A B C Nの展開式の係数 受験の月
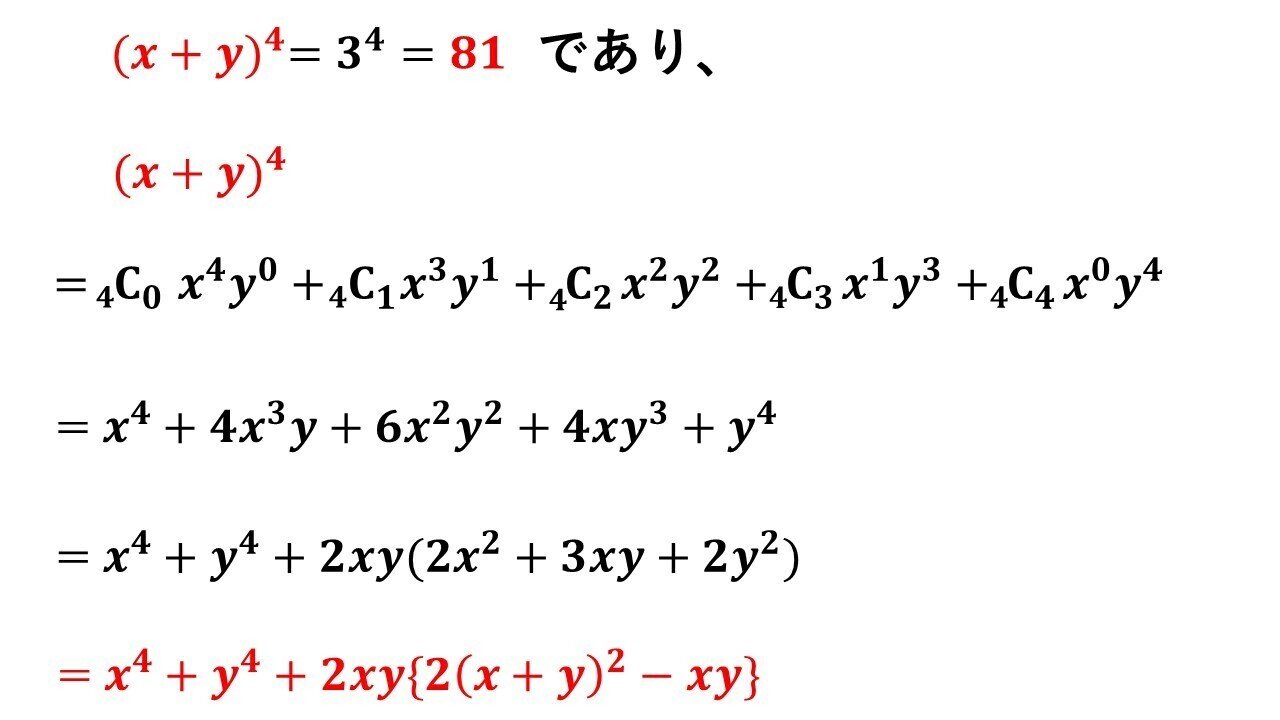



基本対称式の計算問題と二項展開 タロウ岩井の数学と英語 Note




式の乗法 分配法則で展開する問題に慣れよう 中学や高校の数学の計算問題




展開 因数分解を利用する問題 鶴城数人 Note
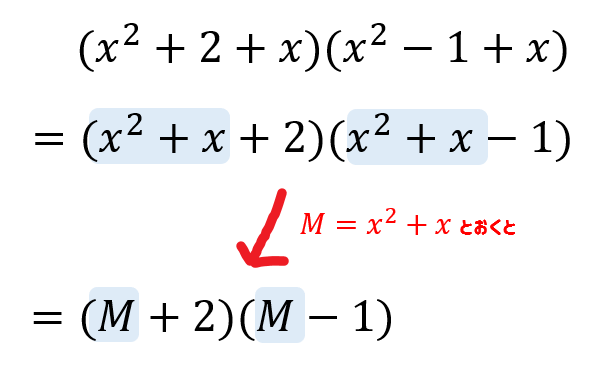



高校数学 式の展開の工夫 置き換えや組み合わせを利用するやり方を解説 数スタ




多項式 4 式の計算を利用して解く バカでもわかる 中学数学



Q Tbn And9gcrkz55leutoiyzt5r9bugl3exoxymmqopzocnnxi6kwx2peohab Usqp Cau




中学数学 多項式 の教え方 展開の応用問題




中3 展開と因数分解2 多項式と単項式の除法 予習 中学数学の勉強に




中学3年生 数学 多項式の乗法と除法 式の展開 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中3 中3 数学 多項式 中学生 数学のノート Clear



1
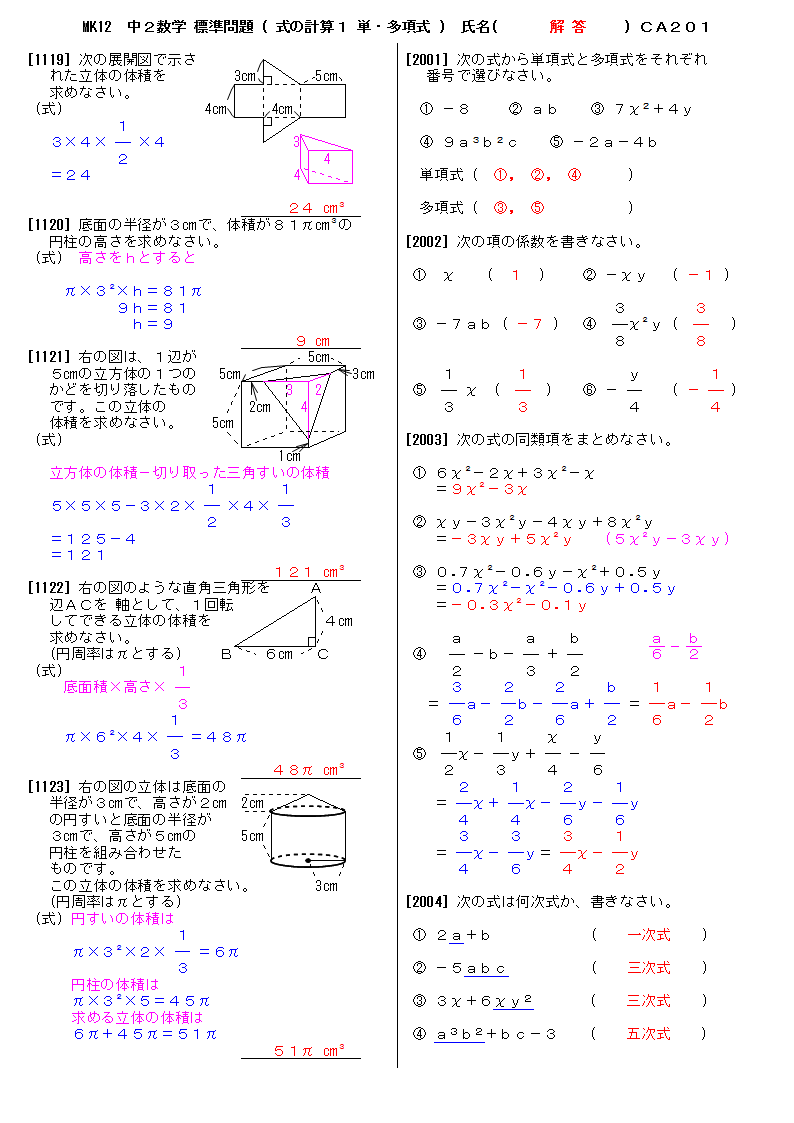



無料 中2数学 標準問題 解答プリント 1 式の計算1 単項式 多項式




中学3年数学講座第1章3多項式 多項式基本問題編 Youtube




中学数学 多項式 の教え方 展開の基本



Studydoctor3項式の展開 中3数学 Studydoctor




中3 中3数学 式の計算 多項式の計算 乗法公式 式の展開 中学生 Clear




多項式の展開公式の説明 おかわりドリル




展開 因数分解を利用する問題 鶴城数人 Note




式の展開 無料で使える中学学習プリント



0 件のコメント:
コメントを投稿